ЛЕКЦИЯ 2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. СТАТИСТИЧЕСКОЕ, ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Классическое определение вероятности

ЛЕКЦИЯ 1. ТЕОРИИ ВЕРОЯТНОСТЕЙ. ИСТОРИЯ ВОЗНИКНОВЕНИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

А.А. Халафян

БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ

1. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и мате-

матическая статистика. М.: Высшая Школа, 1991.

2. Елисеева И.И., Князевский В.С., Ниворожкина Л.И., Морозова З.А. Теория статистики с основами теории вероятностей. М.: Юнити, 2001.

3. Секей Г. Парадоксы в теории вероятностей и математической статистике. М.: Мир, 1990.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2001

5. Смирнов Н.В. Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука,1969.

6. Статистические методы построения эмпирических формул. М.: Высшая Школа, 1988.

ОГЛАВЛЕНИЕ

ЛЕКЦИЯ 1. ТЕОРИИ ВЕРОЯТНОСТЕЙ. ИСТОРИЯ ВОЗНИКНОВЕНИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 3

ЛЕКЦИЯ 2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. СТАТИСТИЧЕСКОЕ, ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 8

ЛЕКЦИЯ 3. АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ. АКСИОМАТИКА КОЛМОГОРОВА.. 14

ЛЕКЦИЯ 4. СЛУЧАЙНАЯ ВЕЛИЧИНА. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.. 17

ЛЕКЦИЯ 5. РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.. 21

ЛЕКЦИЯ 6. ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА–ЛАПЛАСА, ТЕОРЕМА БЕРНУЛЛИ.. 26

ЛЕКЦИЯ 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 29

ЛЕКЦИЯ 8. ПОНЯТИЕ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ... 35

ЛЕКЦИЯ 9. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ... 39

ЛЕКЦИЯ 10. СВОЙСТВА ПЛОТНОСТИ ВЕРОЯТНОСТЕЙ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 43

ЛЕКЦИЯ 11. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН.. 48

ЛЕКЦИЯ 12. ТЕОРЕМА О ПЛОТНОСТИ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН.. 52

ЛЕКЦИЯ 13. РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА, ФИШЕРА .ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.. 57

ЛЕКЦИЯ 14. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН (продолжение) 61

\ЛЕКЦИЯ 15. ВЫЧИСЛЕНИЕ ДИСПЕРСИИ ОСНОВНЫХ РАСПРЕДЕЛЕНИЙ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.. 67

ЛЕКЦИЯ 16. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ МЕРЫ СВЯЗИ СЛУЧАЙНЫХ ВЕЛИЧИН.. 71

ЛЕКЦИЯ 17. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. НЕРАВЕНСТВО ЧЕБЫШЕВА. ЗАКОН БОЛЬШИХ ЧИСЕЛ.. 76

ЛЕКЦИЯ 18. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА.. 79

ЛЕКЦИЯ 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. ПРЕДМЕТ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ. ВАРИАЦИОННЫЕ РЯДЫ... 82

ЛЕКЦИЯ 20. СРЕДНИЕ ВЕЛИЧИНЫ. ПОКАЗАТЕЛИ ВАРИАЦИИ.. 87

ЛЕКЦИЯ 21. ОЦЕНКА ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ.. 93

ЛЕКЦИЯ 22. ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ 97

ЛЕКЦИЯ 23. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. 104

ЛЕКЦИЯ 24. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ.. 107

ЛЕКЦИЯ 25. ЭЛЕМЕНТЫ РЕГРЕССИОННОГО И КОРРЕЛЯЦИОННОГО АНАЛИЗОВ.. 114

БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ.. 122

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

тексты лекций

Краснодар 2008

Принципиально невозможно говорить об абсолютно одинаковых реальных объектах окружающего нас мира и абсолютно одинаковых воздействиях на них, а потому и об абсолютной детерминированности. Все реальные объекты и явления имеют, по-видимому, черты как детерминированного, так и случайного, которые могут проявляться в большей или меньшей степени, поэтому вопрос, а каким является мир на самом деле, в принципе не допускает однозначного ответа.

Например, на основании законов небесной механики по известному в настоящем положению планет Солнечной системы может быть практически однозначно предсказано их положение в любой наперед заданный момент времени, в том числе очень точно могут быть предсказаны солнечные и лунные затмения. Это пример детерминированных законов [1]. Но не все явления окружающего нас мира поддаются точному предсказанию, несмотря на то, что наши знания о нем постоянно углубляются и расширяются. Например, долговременные изменения климата, кратковременные изменения погоды, землетрясения и другие природные катаклизмы не являются объектами для успешного прогнозирования.

Еще менее детерминированными являются некоторые законы и явления микромира. Например, нельзя говорить о точном положении электрона в определенный момент времени, но можно лишь говорить о его распределенном положении в пространстве (электронное облако). Такого рода законы называются статистическими. Согласно этим законам, будущее состояние системы определяется не однозначно, а лишь с некоторой вероятностью [1].

Но в макромире и микромире существуют явления, состояние которых в перспективе предсказать невозможно даже с определенной вероятностью. Такие явления можно назвать неопределенными, например, длительность боевых действий при вооруженных конфликтах, количество погибших, число разрушений и т.д.

Теория вероятностей изучает свойства массовых случайных событий, способных многократно повторяться при воспроизведении определенного комплекса условий. Основное свойство любого случайного события, независимо от его природы, – мера или вероятность его осуществления.

Теория вероятностей – математическая наука. Из первоначально заданной системы аксиом вытекают другие ее положения и теоремы. Впервые законченную систему аксиом сформулировал в 1936 г. советский математик академик А.Н. Колмогоров в своей книге «основные понятия теории вероятностей» [1].

По аналогии с макромиром и микромиром, математические модели могут либо быть детерминированными, либо включать случайные факторы. Если эти факторы являются стохастическими, т.е. подчиняются с определенной точностью законам математической статистики, то говорят о стохастических математических моделях.

Так как большинство прикладных задач являются вероятностными по самой своей природе, за последние годы стохастические модели получили широкое распространение. К тому же в некоторых случаях, хотя задача допускает детерминистскую модель, привлечение случайных компонент приводит к более адекватному или к более детальному описанию реального объекта. Например, случайное воздействие иногда можно полностью игнорировать (если оно не слишком велико), в других случаях его можно учесть максимально возможным значением или принять для него какую-либо детерминированную схему, но наиболее естественно так и считать это воздействие случайным, т.е. принять для его описания стохастическую модель. Наконец, случайные компоненты могут быть искусственно введены в чисто детерминированную модель из-за преимуществ при решении математической задачи, например, при вычислении интегралов по области сложной формы и высокой размерности по методу Монте–Карло [2].

Слабым звеном при использовании стохастических моделей является выбор статистических гипотез о вероятностных характеристиках входных случайных величин и функций. Такие характеристики часто считаются либо полностью известными (например, принимается, что исходная величина распределена по нормальному закону с известными параметрами), либо доступными определению. Однако в реальных ситуациях чаще всего оказывается, что нужная информация отсутствует; более того, во многих случаях ситуация является не стохастической, а неопределенной.

Тем не менее, одна из основных тенденций современной математики и ее приложений состоит в резком повышении роли тех разделов науки, которые анализируют явления, имеющие случайный характер, и основываются на теории вероятностей. И всего лишь небольшим преувеличением прозвучала шутка американского математика Дж. Дуба, начавшего свой доклад в Московском математическом обществе словами: «Всем специалистам по теории вероятностей хорошо известно, что математика представляет собой часть теории вероятностей». Эта тенденция объясняется тем, что большинство возникших в последние десятилетия новых математических дисциплин, оказались тесно связанными с теорией вероятностей. При этом возникновение ряда новых, в большинстве своем «порожденных» теорией вероятностей, наук (например, теория игр, теория информации) привело к положению, при котором теорию вероятностей также приходится рассматривать как объединение большого числа разнородных и достаточно глубоко развитых математических дисциплин [2].

Математическая статистика разрабатывает математический аппарат установления статистических закономерностей и получения научно обоснованных выводов о массовых явлениях из данных наблюдений или экспериментов.

С учетом сказанного можно определить теорию вероятностей и математическую статистику как математическую науку, выясняющую закономерности, которые появляются при взаимодействии большого числа случайных факторов.

Теория вероятностей вначале развивалась как прикладная дисциплина. По-видимому, будет верным утверждение, что теория вероятности обязана своему появлению азартным играм. Хотя сегодня теория вероятностей с азартными играми имеет столько же общего как геометрия с измерением площадей. Игра в кости была самой популярной азартной игрой до конца Средних веков. Слово «азарт» происходи от арабского слова «alzar», переводимого как «игральная кость». Согласно греческой легенде, игру в кости предложил Паламедей для развлечения греческих солдат, скучающих при ожидании битвы при Трое (V в. век до н. э.).

Возможно, игра в кости была известна значительно раньше. Так Дж. Нейман в своей книге «Вводный курс теории вероятностей и математической статистики» пишет, что археологи обнаружили в гробнице фараона две пары костей: «честные» (с равными вероятностями выпадения всех граней) и фальшивые (с умышленным смещением центра тяжести, что увеличивало вероятность выпадения шестерок).

Карточные игры появились в Европе лишь в XIV в., в то время как игра в кости пользовалась успехом еще в Древнем Египте во времена 1-й династии, позднее в Греции и Римской империи.

Самой ранней книгой по теории вероятностей является «Книга об игре в кости» Джордано Кардано (1501–1576). Эта книга была опубликована лишь в 1663 г., спустя 100 лет после написания. Аналогичный трактат был написан Галилеем между 1613 и 1624 г.

Ключевыми моментами развития теории вероятностей были парадоксы, возникающие при попытках моделирования азартных игр. Рассмотрим некоторые из них [3].

Парадокс 1. Игральная кость при бросании с равной вероятностью падает на любую из граней 1, 2, 3, 4, 5, 6. Когда бросают две кости, сумма выпавших очков заключена между 2 и 12. Как 9, так и 10 из чисел 1, 2, 3, 4, 5, 6 можно получить двумя различными способами:

9 = 4 + 5 = 6 + 3;

10 = 5 + 5 = 4 + 6.

В задаче с тремя костями 9 и 10 получаются шестью способами.

Почему тогда 9 появляется чаще, когда бросают две кости, а 10 – чаще, когда бросают три кости. Несмотря на простоту задачи, некоторым великим математикам не удавалось ее решить, так как они забывали о необходимости учета порядка выпадения костей. Ошибались и Лейбниц и Даламбер.

Парадокс 2. Однажды Даламберу задали вопрос: с какой вероятностью монета, брошенная дважды, по крайней мере один раз выпадет гербом вверх. Ответ ученого был 2/3. Ошибкой Даламбера было то, что он рассматривал три возможных исхода (ГР, РР, ГГ) вместо четырех (ГР, РГ, РР, ГГ).

Парадокс 3. Задача шевалье де Мере. Одновременно подбрасываются две кости. Какова вероятность того, что в двадцати четырех подбрасываниях две шестерки выпадут, по крайней мере, 1 раз. По его подсчетам эта вероятность больше 1/2. Но, играя длительное время, он почему-то проигрывал. Шевалье обратился за помощью к Блезу Паскалю, который решил ее и показал, что эта вероятность равна 0,49. Эта задача была также решена Пьером Ферма. Дата опубликования Паскалем решения этой задачи (1654 г.) считается днем рождения науки «Теория вероятностей».

Введем ряд простых определений.

Испытание – это ситуация с более чем одним возможным исходом.

Исход – это результат наблюдения или измерения.

Единичный (отдельный) исход называется элементарным событием.

Набор всех элементарных событий некоторого испытания называется множеством элементарных событий.

Событие определим как подмножество множества элементарных событий.

Достоверное событие – это событие, которое при выполнении определенного комплекса условий обязательно произойдёт.

Невозможное событие – это событие, которое при выполнении определенного комплекса условий никогда не произойдёт.

Случайное событие – это событие, которое при выполнении определенного комплекса условий, может как произойти так и не произойти. Мера возможности осуществления такого события и есть его вероятность.

Будем случайные события обозначать прописными латинскими буквами A, B, C…; достоверное событие обозначим W, невозможное – Æ.

Два события A и B называются несовместными, если появление одного из них исключает появление другого.

Суммой двух событий A и B называется третье событие C = A + B, которое происходит тогда, когда наступает либо событие А, либо событие В, либо оба одновременно. Это определение равносильно другому определению: суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

Пример: А – выпадение четных чисел на игральной кости, В – выпадение чисел кратных 3, тогда С – выпадение чисел 2, 3, 4, 6.

Произведением двух событий A и B называется третье событие C = AB, которое происходит тогда, когда происходит и событие A, и событие B.

Пример: А – выпадение четных чисел на игральной кости, В – выпадение чисел кратных 3, С – выпадение числа 6.

Событие 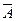называется противоположным событиюA, если оно не совместно с A и вместе (в сумме) образуют достоверное событие, т.е. 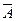+А = W.

Пример: А – выпадение четных чисел на игральной кости, 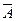– выпадение нечетных чисел.

Классическое определение вероятностиосновывается на равновозможности любого из конечного числа исходов и на предположении, что события составные, т.е. состоят из одного или большего числа элементарных событий (исходов).

Так, например, при бросании игральной кости равновозможно выпадение любого из чисел 1, 2, 3, 4, 5, 6. Обозначим эти исходы w₁, w₂, w₃, w₄, w₅, w_6.Естественно, что шанс осуществится не одному исходу, а одному из двух, например или w₃, или w₆, в два раза больше. Рассуждая, таким образом, можно определить шансы осуществления любого составного события, состоящего из нескольких элементарных событий.

В общем случае, когда имеется n равновозможных исходов w₁, w₂…w_n, вероятность наступления любого события A, состоящего из m исходов w_i₁, w_i₂…w_im, определяется как отношение числа исходов благоприятствующих наступлению события A, к общему числу:

P(A) = m/n.(1)

Так, при бросании игральной кости событие А – выпадение четных чисел, состоит из трех исходов – w₂, w₄, w₆. Поэтому P(A) = 3/6 =1/2.

Событие W^', включающее все исходы называется полным. Тогда по формуле (1)

P(W^') = n/n = 1,

т.е. полное событие является достоверным, так как оно обязательно произойдет, следовательно W = W^' и P(W) = 1, т.е. вероятность достоверного события равна 1.

Задачи:

1. Из 10 автомобилей производства Волжского автомобильного завода 8 с дефектами. Определить вероятность того, что из 5 приобретенных дилерами автомобилей все автомобиля окажутся с дефектами.

Решение. Р =

2. Брошены 2 игральные кости. Найти вероятность того, что сумма выпавших очков равна 10, а разность 2.

Решение.Р =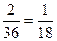

Если события рассматривать как подмножества множества событий, то введенные в лекции 2 отношения между событиями можно интерпретировать как отношения между множествами:

– несовместные события – это такие события (подмножества), которые не содержат общих элементов;

– сумме и произведению событий соответствуют объединение и пересечение

A + B = A È B, AB = A Ç B;

– противоположное событие к А – это дополнение подмножества А, ;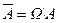

– запись А Ì В означает, что в В содержатся все элементарные события из А и могут содержаться элементарные события, не входящие в А. Если A Ì В и В Ì А, то А = В.

Теорема 1 (сложения вероятностей).Если два составных события А = {w_i₁, w_i₂… w_im} и В = {w_i₁, w_i₂… w_i_к} являются несовместными, то

P(A + B) = P(A È B) = P(A) + P(B) (1)

Доказательство.Так как события A и B несовместны, событие A + B состоит из m + k элементов. При этом все множество элементарных событий состоит из n элементов. Тогда по классическому определению вероятности

P(A + B) = (m + k)/n = m/n + k/n = P(A) + P(B).

Событие 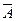, противоположное событию А, можем определить как подмножество, в которое входят все элементарные события, не входящие в А, т.е. А È 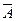= W и А Ç 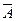= Æ. Тогда из теоремы сложения вероятностей вытекает, что Р(W) = Р(А) + Р(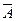) = 1, следовательно,

Р(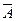) = 1– Р(А) (2)

Из (2) следует, что вероятность невозможного события, являющегося противоположным к достоверному событию (W = W + Æ, W Ç Æ =Æ), равна 0, так как

Р(Æ) = 1 – Р(W) = 0.

Теорема 2 (сложения вероятностей совместных событий).Если два составных события являются совместными, то вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A + B) = P(A È B) = P(A) + P(B) – Р(АВ).

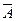Доказательство. Нетрудно видеть, что А + В можно представить в виде суммы трех несовместных событий (рис.1): А + В = А+В + АВ.

Рис. 1

Тогда по теореме 1 имеем

Р(А + В) = Р(А) + Р(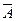В) + Р(АВ) (3)

Учитывая, что

А = А+ АВ, Р(А) = Р(А) + Р(АВ),

имеем

Р(А) = Р(А) - Р(АВ),

аналогично

Р(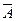В) = Р(В) – Р(АВ).

Подставляя полученные выражения в (3), получим

Р(А + В) = Р(А) – Р(АВ) + Р(В) – Р(АВ) + Р(АВ) = P(A) + P(B) – Р(АВ).

Можно доказать иначе. Нетрудно видеть, что событие A + B состоит из (m + + k – r) элементов, тогда по формуле (1, лекция 1):

P(A + B) = (m + k - r)/n = m/n + k/n – r/n = P(A) + P(B) – P(AB).

При определении вероятности наступления события A предполагается выполнение определённого комплекса условий. Очевидно, что при изменении комплекса условий изменится и вероятность Р(А). Так, если к комплексу условий, при котором определяли Р(А), добавить новое условие, состоящее в появлении события В, то получим другое значение вероятности, которое обозначим P(A/B) = P_B(A). Вероятность P(A/B) называется условной вероятностью наступления события A, при условии, что произойдет событие В. Вероятность Р(А) называется безусловной вероятностью.

Пусть A и В – подмножества элементарных событий, состоящие из m и k элементов (рис. 2).

Рис.2

Тогда по классическому определению вероятностей Р(А) = m/n, Р(В) = k/n.

Пусть событию А при условии, что произойдет событие В благоприятствует r исходов, очевидно, что такими исходами могут быть только исходы принадлежащие А Ç В. Тогда, согласно формуле (1, лекция 1)

P(a/b) = r/k . (4)

Разделим числитель и знаменатель полученной дроби на n

P(a/b) = (r/n)/(k/n) = Р(АÇВ)/Р(В), т.е.

P(a/b) = Р(АÇВ)/Р(В). (5)

Формула (5) называется формулой нахождения условной вероятности наступления события А при условии, что произойдет событие В.

Пример. Бросаем игральную кость. Пусть событие А состоит в выпадении числа очков, кратных 3, т.е. А = {3, 6}, а событие В – в выпадении четного числа очков, т.е. В = {2, 4, 6}. Тогда А Ç В ={6}, Р(А Ç В) = 1/6, Р(В) = 3/6 =1/2 и P(a/b) = (1/6)/(1/2) = 1/3. В то же время r = 1, k = 3 и если считать по формуле (3), также получим P(a/b) = r/k = 1/3.

Определение 1. Событие A называется независимым от события B, если его условная вероятность равна безусловной, т.е.

P(A) = P_B(A) = P(a/b). (6)

Из (5) следует

P(AB) = Р(АÇВ) = P(A/B)P(B). (7)

Фрмула (7) называется формулой умножения для зависимых событий.

Из (6) и (7) следует

P(AB) = P(A) P(B) (8)

Формула (8) называется теоремой умножения для независимых событий.