Маршруты в графах

Маршрутом в произвольном графе называется чередующаяся последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной. В простом графе маршрут однозначно определяется только последовательностью вершин. Будем рассматривать следующие конечные маршруты, которые часто используются в задачах обхода графа: цепи, циклы и пути.

Для неориентированных графов справедливы следующие понятия.

Цепь – последовательность ребер S = (g₁, g₂, ..., g_n), в которой у каждого ребра g_k одна из вершин явля­ется вершиной ребра g_k-1, а другая - вершиной ребра g_k+1. При этом одно и то же ребро или вершина может встречаться несколько раз. Пример цепи для графа (рис. 3.6):

S = (g₀, g_l, g₂, g₃, g₄, g₅, g₂, g_б) = ((x₀, х₁), (х₁, х₂), (х₂, х₃), (х₃, х₁), (х₁, х₄), (х₄, х₃), (х₃, х₂), (х₂, х₅)).

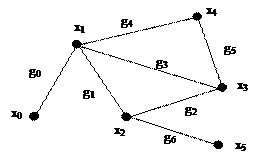Рис. 3.6. Пример цепи

Цепь называется про­стой, если все ребра в ней раз­личны, и сложной (составной) – в противном слу­чае. Вершины в простой цепи могут повторяться.

Цепь назы­вается элементарной, если в ней ни одна из вершин не повторяется.

Циклом называется конечная цепь, начинающаяся на некото­рой вершине х_i, и окачивающаяся на ней же. Простые, сложные и элементарные циклы определяются по аналогии с цепями.

Для ориентированных графов введены следующие дополни­тельные понятия.

Путем в графе G(X) называется такая последовательность дуг (g_l, g₂, …), что конец каждой предыдущей дуги является началом следующей. Существуют простые, сложные и элементар­ные пути.

Х|

Х0

Контур графа – это конечный путь, у которого начальная вер­шина совпадает с конечной. Существуют простые, слож­ные (составные) и элементарные контуры.

Длина пути есть число дуг L(s) в последовательности дуг пути s. В случае бесконечного пути L(s) = ¥.

Граф называется симметрическим, если " x_i, x_j из того, что x_i Î G(x_j) Þ x_j Î G(x_i), то есть две смеж­ные вершины x_i, x_j всегда соединены противоположно ориентирован­ными дугами (рис.3.7).

 

 

Рис. 3.7. Симметрический граф

 

Граф называется антисимметрическим, если " x_i, x_j
x_i Î G(x_j) Þ x_j Ï G(x_i), то есть каждая пара смежных вершин соединена только в одном направлении.

Граф называется конечным, если число его вершин конечно и бесконечным, если число вершин бесконечно. Граф G(X) называется G – конечным, если для каждой его верши­ны х Î X множество G(x) конечно.