Доверительный интервал для генеральной средней и генеральной доли по большим выборкам

 

Рассмотрим большие выборки (порядка сотен наблюдений).

Теорема. Вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдёт по абсолютной величине число , равна:

, ;

, . -

формулы доверительной вероятности для средней и доли.

 

Где - функция Лапласа, и - среднеквадратические отклонения выборочной средней и выборочной доли или среднеквадратические ошибки выборки (собственно случайная повторная выборка). Если выборка бесповторная, то среднеквадратические отклонения выборочной средней и выборочной доли - и .

	Повторная выборка	Бесповторная выборка
Средняя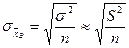
Доля

Формулы для нахождения среднеквадратических ошибок выборки запишем в таблицу.

При малом объеме выборки 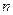величина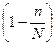 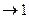, поэтому значения для среднеквадратических ошибок при повторной и бесповторной выборке приблизительно равны между собой.

 

Следствия теоремы:

1) при заданной доверительной вероятности 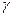предельная ошибка выборки

,

, где .

2) доверительные интервалы для генеральной средней и генеральной доли могут быть найдены по формулам

,

.

 

Пример 9.1.Для определения средней урожайности пшеницы на площади 10000 Га определена урожайность на 1000 Га. Результаты выборки приведены в таблице:

Урожайность, ц/Га	11-13	13-15	15-17	17-19
Количество, Га

 

Найти:

1) вероятность того, что средняя урожайность пшеницы на всём массиве отличается от средней выборочной не более чем на 0,1 ц, если выборка:

а) повторная;

б) бесповторная;

2) границы, в которых с вероятностью 0,9973 заключена средняя урожайность на всём массиве.

Решение. Вычислим выборочную среднюю и выборочную дисперсию.

Середины интервалов равны: .

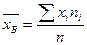
ц.

,

 

Исправленная дисперсия .

1) Запишем формулу доверительной вероятности для выборочной средней

.

а) Если выборка повторная, то , где , .

Найдем . Т.о. , а доверительная вероятность

.

б) Если выборка бесповторная, то , где .

Найдем .

Т.о. , а доверительная вероятность

.

2) Средняя урожайность на всём массиве заключена в границах:

.

По условию

Предельная ошибка выборки: ц. – выборка повторная,

ц. – выборка бесповторная.

Таким образом с вероятностью 0,9973 средняя урожайность на всём массиве заключена в границах: , т.е. - выборка повторная,

, т.е. - выборка бесповторная.

 

9.3. Объём выборки

 

Для проведения выборочного наблюдения важно правильно установить объём выборки 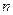при заданных величинах надёжности оценки 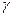и точности оценки 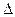. Объём выборки находится из формул предельной ошибки выборки: - при оценке генеральной средней или - при оценке генеральной доли.

Формулы для нахождения объема выборки представлены в таблице.

	Повторная выборка	Бесповторная выборка
Средняя
Доля

 

Если найден объём повторной выборки 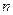, то объём бесповторной выборки можно определить по формуле

.

Так как , то .

Пример 9.2. По условию примера 9.1. определить объём выборки, при котором с вероятностью 0,9973 отклонение средней урожайности в выборке от средней урожайности на всей площади посева не превзойдет 0,5 ц (по абсолютной величине).

Решение. Если выборка повторная, то ее объем .

В качестве берём состоятельную оценку ;

так как по таблице . Таким образом .

Объем бесповторной выборки .