Двумерный нормальный закон распределения

Свойства коэффициента корреляции

1) .

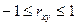2) Если и - независимые случайные величины, то .

3) Если случайные величины и связаны линейной зависимостью, то .

 

Определение.Случайная величина называется распределенной по двумерному нормальному закону, если ее совместная плотность имеет вид:

 

,

 

где .

Из определения следует, что двумерный нормальный закон распределения определяется пятью параметрами: .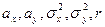

Параметры 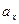и выражают математические ожидания случайных величин и , параметры и 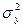- их дисперсии, а - коэффициент корреляции между случайными величинами и .

 

Плотности вероятности одномерных случайных величин и равны:

 

, .

 

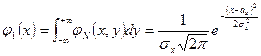Каждый из законов распределения одномерных случайных величин и является нормальным с параметрами соответственно 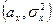и .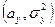

Найдём условные плотности вероятности случайных величин и по формулам:

 

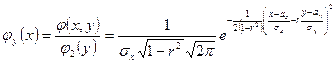и аналогично

.

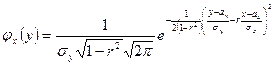Каждый из условных законов распределения случайных величин и является нормальным с условным математическим ожиданием и условной дисперсией, определяемыми по формулам:

, ,

, .

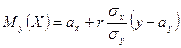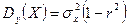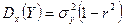Из этих формул следует, что линии регресси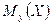и и нормально распределенных случайных величин представляют собой прямые линии, то есть нормальные регрессии по и по всегда линейны.

Условные дисперси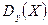и и 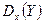(а значит и условные стандартные отклонения 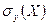и 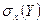) постоянны и не зависят от значений и .