Интегральная теорема Муавра-Лапласа

 

Теорема. Если вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что событие появится в 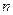испытаниях от дораз, приближённо равна

,

где , , - функция Лапласа.

 

Существует таблица значений функции , которая приводится в приложениях учебников.

 

Свойства функции:

1) Нечётная: .

2) -возрастающая функция.

3) При функция приближается к 1. Поэтому в таблице для приведены значения лишь до , так как при можно принять, что .

Пример 3.3. Вероятность попадания в цель из скорострельного орудия при отдельном выстреле равна 0,75. Найти вероятность того, что при 300 выстрелах число попаданий будет не менее 210, но не более 230 раз.

 

 

Решение. По условию n = 300, p = 0,75, q = 0,25, k₁ = 210, k₂ = 230.

Используем интегральную теорему Муавра – Лапласа.

Имеем , .

Тогда , =.

Следовательно,

.

 

Рассмотрим следствие интегральной теоремы Муавра-Лапласа.

Следствие. Если вероятность наступления события в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе 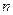независимых испытаний

а) вероятность того, что число наступлений события отличается от произведения не более, чем на величину (по абсолютной величине), т.е.

.

б) вероятность того, что частота события заключена в пределах от до (включительно), т.е.

,

где , .

в) вероятность того, что частота события отличается от его вероятности не более, чем на величину (по абсолютной величине), т.е.

.

Пример 3.2. Вероятность события в отдельном испытании . Найти вероятность того, что при 150 испытаниях частота появления этого события будет отличаться от его вероятности не более, чем на 0,03.

Решение. .

 

Тема 4. Дискретная случайная величина и её характеристики