Суммирующие счетчики

Такты

LMBD

SET

SAT

EXTU

EXT

CLR

Сервисные команды

Команда перехода

Особенность команды: в слотах задержки можно разместить другие команды.

       
 
Такт (выполняемый пакет) Командная строка
B .S2 L0
ADD .L1 A1,A2,A3 || ADD .L2 В1,В2,В3
2 (6) L0: MPY .M1X A3,B3,A4 || SUB .D1 A5,A6,A6
3 (7) MPY .M1 A3,A6,A5
MPY .M1 A6,A7,A8
SHR .S1 A4,15,A4
  ADD .D1 A4,A6,A4

 
   
 

 


пакет выборки

 

CLR .S1 A1,5,19,A2 границы области: (нижняя) a = 5, (верхняя) b = 19.

перед командой после 1 такта 2h Ch 1h Ah

А1 9D12 C1A4h 9D12 C1A4h 9D10010 1100 0001 10104

A2 xxxx xxxxh 9D10 0004h

 

CLR .S1 A1,A2,A3

Перед командой после 1 такта b a

А1 9D12 C1A4h 9D12 C1A4h 10 младших бит А2: 1110 0110 0101

A2 0000 0265h 0000 0265h а = 001012 = 510

A3 xxxx xxxxh 9D10 0004h b = 100112 = 1910

 

Границы области вычисляются по константам, указанным в команде: нижняя а = k2-k1, верхняя b = 31-k1.

EXT .S1 A1,10,19,A2 a = 19-10 = 9, b = 31-10 = 21.

перед командой после 1 такта Ah 4h 3h Fh

А1 07А4 3F2Ah 07А4 3F2Ah 07 1010 0100 0011 11112A

A2 xxxx xxxxh FFFF F21Fh 1…………….1001000011111

 

EXT .S1 A1,A2,A3 k1 k2

перед командой после 1 такта 10 младших бит А2: 00 0111 0011

А1 03В6 E7D5h 03В6 E7D5h k1 = 00 0112 = 310

A2 0000 0073h 0000 0073h k2 = 1 0011 = 1910

A3 xxxx xxxxh 0000 03B6h a = 19-3 = 16, b = 31-3 = 28.

 

 

Правило формирования результата:

- если N > 231-1 (7FFF FFFFh), результат равен 231-1;

- если N < -231 (-00:8000 0000h или в дополнительном коде FF:8000 0000 h), результат равен -231 (8000 0000h);

- иначе результат равен N.

 

SAT A1:A0,А3

перед командой после 2 тактаКомментарий:

A1:A0 0000 001Fh:3413 539Ah 0000 001Fh:3413 539Ah N > 231-1

А3 xxxx xxxxh 7FFF FFFFh

 

SAT A1:A0,А3

перед командой после 2 тактаКомментарий:

A1:A0 0000 00FFh:7000 0000h 0000 00FFh:7000 0000h N < -231

А3 xxxx xxxxh 8000 0000h

 

SAT A1:A0,А3

перед командой после 2 тактаКомментарий:

A1:A0 0000 00FFh:A190 7321h 0000 00FFh: A190 7321h -231 < N < 231-1

А3 xxxx xxxxh A190 7321h

 

SET .S1 A0,7,21,A1 a = 7, b = 21.

перед командой после 1 такта1h 3h 4h Ah 1h

А0 4B13 4A1Eh 4B13 4A1Eh 4B 0001 0011 0100 1010 0001 E

А1 xxxx xxxxh 4В3F FF9Еh 4B 0011 1111 1111 1111 1001 E

 

SET .S2 В0,В1,В2

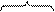перед командой после 1 такта a b

В0 9ED3 1A31h 9ED3 1A31h 10 младших бит B1: 01 1001 0111

В1 0000 С197h 0000 С197h a = 011002 = 1210 b = 101112 = 2310

В2 xxxx xxxxh 9EFF FA31h 9E 1101 0011 0001 A31

 

Значение младшего бита первого из указанных в команде регистров определяет предмет поиска во втором регистре – первую слева 1 или первый слева 0.

 

LMBD L1. A1,A2,A3

Перед командой после 1 такта

А1 0000 0001h 0000 0001h (в А2 определить число нулей до первой слева 1)

А2 009E 3A81h 009E 3A81h

A3 xxxx xxxxh 0000 0008h

 

 

4.7. Ограничения целостности ресурса

 

 
 

Ограничения на использование командами одного и того же функционального

устройства

 
 

Ограничения на перекрестные линии (1X и 2X)

 

 
 

Ограничения на чтения регистра

 

 
 

Ограничения на записи в регистр

 

Ограничения на загрузку и хранение

 
 

 
 

Конфликты множественной записи

 
 

 

 

Для передачи каждого бита информации отводится одинаковый интервал времени, называемый тактом. Любое цифровое устройство тактируется. При этом такты задаются генератором тактовой частоты.

Тактирование означает, что входные и выходные двоичные наборы изменяются только в момент начала следующего такта. В течение же такта производится преобразование входного набора в выходной. Т.о., такт определяет скорость обработки информации или, что то же самое, быстродействие ЦУ.

 

В обеих формах сигналы принимают только два значения и потому называются двоичными сигналами. В этой терминологии КЦУ определяется следующим образом:

комбинационным называется цифровое устройство, у которого выходные двоичные сигналы в любой момент времени зависят только от тех двоичных сигналов, которые поступают на вход устройства в тот же момент времени.

Отсюда следует, что сигналы на выходе КЦУ изменяются практически сразу после изменения входных сигналов. Т.е. КЦУ не обладают памятью.

 

Любая задача синтеза ЦУ начинается с определения разрядной сетки, необходимой для обработки десятичных чисел в заданном диапазоне от Мmin до Мmax. Определяется она выражением:

n = ù log2(Мmax + 1) é, где ù x é – наименьшее целое, не меньшее х.

Отсюда легко решается обратная задача: наибольшее десятичное целое, которое можно отобразить в n-разрядной сетке Мmax = 2n – 1. Как видно, Мmin не имеет никакого значения. Тогда, положив Мmin = 0, последнее выражение позволяет определить общее количество (N) двоичных n-разрядных наборов: N = 2n (0 входит в диапазон чисел).

Различают полностью и не полностью (частично) определенные КЦУ. КЦУ называется полностью определённым, если каждому из всех его возможных входных двоичных наборов поставлен в соответствие строго определенный двоичный набор на выходе. Если хотя бы для одного входного набора значение соответствующего выходного набора безразлично, КЦУ называется не полностью или частично определённым.

На практике частично определенным КЦУ соответствуют ситуации, когда некоторые двоичные наборы либо никогда не появляются на входе, либо соответствующие выходные наборы всегда оказываются невостребованными последующими устройствами.

Синтез любого КЦУ проводится в следующей последовательности:

1. Задается закон функционирования.

2. Для каждого из m выходов выводится минимальная ФАЛ, то есть ФАЛ с минимальным числом членов и минимальным числом аргументов в каждом члене.

3. При необходимости каждая минимальная ФАЛ записывается в заданном минимальном базисе.

4. Cтроится структурная схемы устройства.

 

2.2. Способы задания КЦУ

 
 

1. Табличный.

 

2. Скобочная запись таблицы истинности.

полностью определенное частично определенное

 
 

 


 

у/n=3 = [0, 1, 4, 7] у/n=3 = [1, 4, 7, (2, 3, 6)]

у/n=3 = (2, 3, 5, 6) у/n=3 = (2, 3, 6, [1, 4, 7])

 
 

1. Асинхронный.

Принципы построения: 1) тактируется только триггер младшего разряда, 2) выход предыдущего триггера соединяется со счетным входом последующего.

Быстродействие: 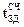=n×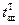. fт £ fтmax = 1/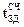. Принцип суммирования: триггер любого старшего разряда переключается, только если триггеры всех младших разрядов установлены в1.

2. Синхронные счетчики.

Принципы построения: 1) тактируются все триггеры, 2) для реализации принципа суммирования добавляется схема формирования переноса.

с последовательным переносом:с параллельным переносом:

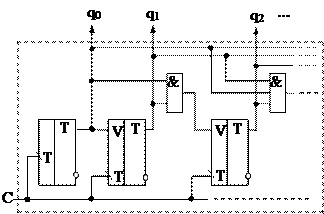
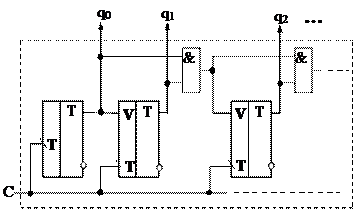
Быстродействие: 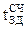= 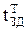+ (n-2)×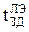; 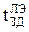<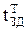. Быстродействие: + .

 

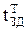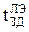Многоразрядный счетчик с параллельно-последовательным переносом:

 

 

 
 

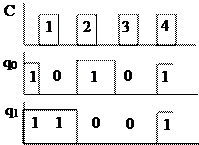Вычитающие счетчики