Арифметические операции над целыми числами.

1. Сложение:

а) производится поразрядно, начиная с младших разрядов;

б) если сумма S_i чисел i-го разряда превышает или равна ОСС, то в этот разряд результата записывается разность (S_i – k×ОСС), а в следующий, более старший разряд (включая и знаковый), переносится k в виде дополнительного слагаемого. Здесь k – целая часть от деления S_i на ОСС.

Например, в случае двоичной системы счисления и S_i = 5, k = [5/2] = 2. Следовательно, в i-й разряд результата запишется 5-k×2 = 5-4 = 1, а в следующий разряд переносится (говорим «в уме») дополнительное слагаемое 2 (k = 2);

в) в случае знаковых чисел перенос из знакового разряда не производится.

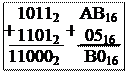Примеры: числа без знака знаковые числа

 

Возможно переполнение Переполнения нет

-5+7 -55₁₆+5₁₆

Результат операции над знаковыми числами представлен в прямом коде, если он положительный и в дополнительном коде, если отрицательный.

 

2. Вычитание заменяется сложением чисел, предварительно представленных в дополнительном коде.

Примеры при n = 4:

6₁₆-3₁₆ = 6₁₆+D₁₆ = 3₁₆ (перенос из знакового разряда не производится);

3₁₆-6₁₆ = 3₁₆+А₁₆ = D₁₆ (дополнительный код числа -3);

-6₁₆-3₁₆ = A₁₆+D₁₆ = 17₁₆ (переполнение разрядной сетки).

 

3. Умножение для положительных чисел выполняется обычным образом, а для отрицательных – с промежуточным преобразованием в прямой код.

 

Примеры: а). Числа без знака:

x

5Е (Е×2=28 28:16=1, остаток 12; С пишем, 1 в «уме»)

А2 (5×2=10 10+1=11)

+

BC (Е×А=140 140:16=8, остаток 12; С пишем, 8 в «уме»)

3AC (5×А=50 (50+8):16=3, остаток 10; А пишем, 3 в «уме»)

3B 7C

б). Знаковые числа: 52 ´ AE = 52 ´ (-52) = -1A44h = E5BC.

 

4.2. Методы адресации операндов (самостоятельно)