Регулирующие устройства и автоматические регуляторы.

ОГЛАВЛЕНИЕ

Раздел 3. Регулирующие устройства, и автоматические регуляторы, исполнительные механизмы, интерфейсные устройства

3.1. Регулирующие устройства и автоматические регуляторы…………………………………..56

3.2. Исполнительные механизмы………………………………………………………………..…79

3.3. Интерфейсные устройства………………………………………………………………….….91

Раздел 3. Регулирующие устройства, и автоматические регуляторы, исполнительные механизмы, интерфейсные устройства

Регулирующие устройства и автоматические регуляторы.

В стандарте DIN 19226 дается следующее определение понятия "регулирующее устройство" и "регулятор":

Регулирующее устройство – это приборы, которые необходимы непосредственно для воздействия на объект регулирования в соответствии с поставленной задачей. В состав регулирующего устройства входят как минимум одно устройство для регистрации регулируемой величины x и для сравнения с задающей величиной w, а также одно устройство для формирования регулирующей величины y.

Регулятор – это прибор, который в рамках регулирующего устройства объединяет в себе выполнение нескольких функций, присущих регулирующему устройству. Однако для регулятора обязательно наличие сравнивающего устройства, а также как минимум еще одного важного функционального элемента, например усилителя или схемы задержки.

Автоматический регулятор - это устройство (совокупность устройств), посредством которого осуществляется процесс автоматического регулирования. Функционирование автоматического регулятора происходит в соответствии с алгоритмом регулирования, под которым понимают математическое выражение функциональной зависимости выходной величины регулятора от входной. Основная задача регуляторов заключается в формировании такого управляющего воздействия на объект регулирования в зависимости от измеренных отклонений регулируемой величины, чтобы восстановить требуемое состояние объекта. Автоматические регуляторы классифицируются по различным признакам (рис.3.1).

В зависимости от возможности изменять свой режим работы регуляторы подразделяются на два класса:

- детерминированные регуляторы не изменяют своих параметров в процессе регулирования;

- регуляторы с настройкой - экстремальные и адаптивные. Экстремальные - непрерывно производят поиск оптимальных значений выходных величин объекта. В адаптивных регуляторах происходит настройка параметров с целью достижения оптимального качества регулирования при изменении характеристик объекта во время его работы.

По наличию дополнительных источников энергии различают регуляторы:

- Регуляторы прямого действия управляют регулирующим органом за счет энергии, получаемой от регулируемой среды, и не требуют вспомогательной энергии.

- Регуляторы непрямого действия. В них имеются усилители мощности, управляющие поступлением энергии от постороннего источника. При этом в зависимости от вида используемой энергии различают электрические, пневматические, гидравлические и комбинированные регуляторы.

В зависимости от характера воздействия на объект имеются:

- регуляторы непрерывного действия - обеспечивают непрерывное изменение регулирующего воздействия. Во многих случаях к ним относят и регуляторы с импульсным перемещением регулирующего органа.

- регуляторы дискретного действия - изменяют регулирующее воздействие только в определенные моменты времени, в интервале между которыми регулирующее воздействие постоянно.

В зависимости от вида квантования входного сигнала подразделяются на:

- релейные;

- импульсные;

- цифровые.

Рис.3.1. Классификация автоматических регуляторов дискретного действия

В соответствии с реализуемым законом регулирования регуляторы делятся на:

- пропорциональные;

- интегральные;

- пропорционально-интегральные;

- пропорционально-дифференциальные;

- пропорционально-интегрально-дифференциальные;

- релейные двух- и трехпозиционные и релейные с механизмами постоянной скорости.

По способности изменять свою структуру различают регуляторы:

- с фиксированной структурой - не изменяют свою структуру при изменении характеристик объектов регулирования;

- с переменной структурой – у них структура изменяется при изменении свойств объекта.

По характеру математической связи между выходной и входной координатами регуляторы подразделяются на:

- линейные;

- нелинейные.

В зависимости от конструктивного исполнения имеютсярегуляторы:

- приборного типа - в системе регулирования включается последовательно со вторичным прибором, в котором формируется сигнал ошибки;

- аппаратного типа - сами формируют сигнал ошибки и обычно включаются параллельно вторичному прибору;

- агрегатного типа – в них используется агрегатный принцип построения используется при стандартных сигналах на выходе датчиков. Такой принцип рекомендован ГСП и позволяет подключать любой стандартизованный датчик непосредственно к унифицированному входу регулятора.

В соответствии с числом регулируемых величин регуляторы подразделяются на:

- одномерные;

- многомерные.

Регуляторы классифицируются также по классу систем и фирмам-изготовителям.

Линейные регуляторы – это регуляторы, которые позволяют реализовать теоретические (стандартные) законы регулирования, называются идеальными. В этих регуляторах операции интегрирования, дифференцирования, суммирования и умножения на постоянный коэффициент выполняются абсолютно точно. Рассмотрим динамические характеристики регуляторов с различными стандартными законами регулирования.

Пропорциональные (П) регуляторы.Закон регулирования П-регулятора выражается уравнением

y = k_px

где k_p - коэффициент пропорциональности, являющийся параметром настройки П-регулятора.

У пропорциональных регуляторов отклонение регулируемой величины X от ее заданного значения Х₀ вызывает перемещение регулирующего органа на величину, пропорциональную этому отклонению x=Х₀-X.

Передаточная функция П-регулятора имеет вид:

W_п(p) = k_p

Переходная характеристика П-регулятора показана на рис.3.2, а.

Величину, обратную коэффициенту пропорциональности регулятора, т.е. δ_р=1/k_р, называют статизмом, или коэффициентом неравномерности регулятора, а величину (1/k_p) 100% -диапазоном дросселирования.

Рис.3.2. Переходные характеристики линейных идеальных регуляторов

Особенностью систем регулирования с П-регулятором является изменение регулируемой величины при различных нагрузках регулируемого объекта. Объясняется это тем, что перемещение регулирующего органа в новое положение, соответствующее новой нагрузке, может быть произведено только за счет отклонения регулируемой величины. Разность между максимальным и минимальным установившимися значениями регулируемой величины ∆х_шах называют остаточной неравномерностью П-регулятора, ее величина определяется выражением ∆х_шах=1/k_p.

Интегральные (И) регуляторы. Процесс регулирования И-регулятором происходит по закону, который описывается уравнением:

где Т_и - постоянная времени интегрирования, являющаяся параметром настройки И-регулятора.

Интегральные регуляторы производят перемещение регулирующего органа пропорционально интегралу отклонения регулируемой величины до тех пор, пока не восстановится ее заданное значение.

Передаточная функция И-регулятора имеет вид:

W_и(р)=1/Т_иp

Переходная характеристика И-регулятора показана на рис.3.2, б. Интегральный регулятор не обладает остаточной неравномерностью, что является его положительной особенностью.

Пропорционально-интегральные (ПИ) регуляторы. Закон регулирования ПИ-регулятора выражается уравнением:

где Т_и— время интегрирования регулятора, или время изодрома. Коэффициент пропорциональности k_p и постоянная времени Т_и являются параметрами настройки ПИ-регулятора.

Уравнение закона регулирования ПИ-регулятора состоит из двух составляющих регулирующего воздействия: k_px - пропорциональной и - интегральной. Передаточная функция ПИ-регулятора имеет вид:

W_ПИ(р) = k_p(Т_иp+1)/Т_иp

В динамическом отношении ПИ-регулятор представляет собой систему из двух параллельно включенных регуляторов: пропорционального и интегрального. При увеличении времени изодрома до бесконечности ПИ-регулятор превращается в П-регулятор. Если k_p и Т_и стремятся к нулю, но их отношение остается постоянным, то получим И-регулятор. Пропорционально-интегральные, как и интегральные, регуляторы не обладают остаточной неравномерностью. Переходная характеристика ПИ-регулятора показана на рис.3.2, в.

Пропорционально-дифференциальные(ПД) регулятор.Закон регулирования ПД-регулятора выражается следующим уравнением:

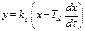
где Т_д - время дифференцирования, или время предварения регулятора, характеризующее степень влияния воздействия по производной на величину регулирующего воздействия. Коэффициент пропорциональности k_p и постоянная времени Т_д ПД-регулятора являются параметрами его настройки. Передаточная функция ПД-регулятора:

W_ПД(р) = k_p(1+Т_дp)

Пропорционально-дифференциальный, как и пропорциональный, регулятор обладает остаточной неравномераостью, величина которой определяется выражением ∆х_шах=1/k_р.

Однако дополнительное воздействие по скорости отклонения регулируемой величины от заданного значения положительно влияет на процесс регулирования. Это является преимуществом ПД-регуляторов по сравнению с П-регуляторами. Переходная характеристика ПД-регулятора показана на рис.3.2, г.

Пропорционально-интегрально-дифференциальные (ПИД) регуляторы. Закон регулирования ПИД-регулятор а определяется уравнением:

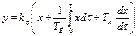
Параметрами настройки ПИД-регулятор а служат коэффициент пропорциональности k_р и постоянные времени Т_я и Т_я. Передаточная функция имеет вид:

W_ПИД(р) = k_p(Т_дТ_иp + Т_иp + 1)/Т_иp

В динамическом отношении эти регуляторы представляют собой систему из трех параллельно включенных звеньев: безынерционного, интегрирующего и идеального дифференцирующего. При Т_Д = 0 ПИД-регулятор превращается в ПИ-регулятор. ПИД-регуляторы не обладают остаточной неравномерностью. Переходная характеристика ПИД-регулятора показана на рис.3.2, д

Промышленные регуляторы состоят из реальных элементов, поэтому их динамические характеристики отличаются от динамических характеристик, определяемых уравнениями идеальных регуляторов.

Для оценки расхождения характеристик идеального и реального регуляторов передаточную функцию W_p(p) реального регулятора представляют в виде произведения передаточной функции W_ид(р) идеального регулятора и передаточной функции W_б(p) некоторого балластного звена:

W_р(р)=W_ид(р)W_б(р)

Балластное звено не имеет заранее известной передаточной функции. Разные регуляторы имеют балластные звенья с различными передаточными функциями. С помощью понятия «балластное звено» удобно оценить степень отличия реального и соответствующего идеального регуляторов. В ряде случаев, анализируя балластное звено, можно найти способы приблизить реальный регулятор к идеальному, усовершенствуя его схему или конструкцию. Исследование динамики балластного звена позволяет сделать вывод об особенностях структурной схемы и настройки того или иного реального регулятора.

Если регулятор идеальный, то передаточная функция балластного звена W₆(ρ)≡1, его модуль W₆(ω)≡1, а фаза φ₆(ω)≡0. Чем больше передаточная функция балластного звена отличается от единицы, тем значительнее отличается качество регулирования в системах с идеальными и реальными регуляторами. Степень отличия реального регулятора от идеального для одного и того же типа прибора может быть различной, так как она зависит не только от структурной схемы и конструкции, но и от динамических настроек регулятора. Для регуляторов с нелинейными элементами частотные характеристики балластного звена зависят также от амплитуды входного сигнала.

Область в пространстве амплитуд, частот входного сигнала и параметров настройки регулятора, в пределах которой частотные характеристики идеального и реального регуляторов отличаются на величину, не превышающую некоторое наперед установленное значение, называют областью нормальной работы (ОНР) регулятора.

Частотные характеристики идеального и реального регуляторов согласно установленным нормам могут отличаться по модулю на ±10% и по фазе на ±15%. В пределах этих отклонений различием в динамических характеристиках можно пренебречь, а в расчетах использовать уравнения идеальных регуляторов.

Сопоставление по величине ОНР является удобным и наглядным методом оценки регуляторов, отрабатывающих одинаковый закон регулирования. Обычно оно проводится при одних и тех же заранее выбранных значениях, амплитуды и частоты входного сигнала в координатах параметров настройки регуляторов.

При оценке регулятора обычно исходят из того, что егоприменение целесообразно, если оптимальные значения параметров настройки, лежащие внутри ОНР, соответствуют динамическим характеристикам объектов управления. Из двух однотипных регуляторов, имеющий большую ОНР лучше, так как он в большей мере удовлетворяет требованиям универсальности, поскольку может быть использован на более широком классе объектов.

Если в результате расчета параметров настроек регулятора будут получены данные, не попадающие в ОНР, то нужно выбрать либо другой закон регулирования, либо применить регулятор другого типа, имеющий более широкую область допустимых настроек.

Автоматические регуляторы, формирующие один и тот же закон регулирования, могут быть построены по различным структурным схемам. Каждая из таких структурных схем обладает рядом достоинств и недостатков, которые необходимо учитывать при разработке регуляторов и при их эксплуатации. Анализ структурных схем позволяет не только оценить, насколько характеристики реального регулятора отличаются от характеристик идеального, но и установить причины этих отклонений. Рассмотрим некоторые структурные схемы.

1. П-регуляторы. Типичная структурная схема пропорционального регулятора (рис.3.3, а) состоит из усилительного и интегрирующего звеньев, охваченных жесткой отрицательной обратной связью. Интегрирующим звеном является исполнительный механизм, который служит для преобразования выходного сигнала регулирующего блока в механическое перемещение.

Если усилитель k₁ считать безынерционным с конечным значением коэффициента усиления, а исполнительный механизм - идеальным интегрирующим звеном, то передаточная функция регулятора запишется в виде:

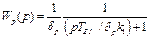
Рис.3.3. Структурная схема и переходные характеристики реального линейного П-регулятора

где Т_ИM - постоянная времени исполнительного механизма. Обозначим Т_б = Т_ИM/δ_pk₁ тогда передаточная функция балластного звена:

W₆(p)=1/(T₆p+1)

Таким образом, реальный регулятор, для которого справедливы названные допущения, можно представить в виде последовательного соединения идеального П-регулятора с коэффициентом усиления k_p и балластного звена с передаточной функцией W₆(p).

Балластное звено в этом случае будет представлять собой апериодическое звено первого порядка с постоянной времени Т_б, величина которой растет с увеличением постоянной времени исполнительного механизма Т_им и коэффициента пропорциональности регулятора k_р. Наличие балластного звена в П-регуляторе объясняется конечным значением коэффициента усиления k₁. Действительно, если k₁→∞, то Т_б→0, a W_p(p)=k_p=W_П(p), т.е. рассматриваемый регулятор становится идеальным. На рис. 88, б приведены переходные характеристики П-регулятора с балластным звеном при различных значениях Т_б.

2. ПИ-регуляторы. Имеется несколько разновидностей схем ПИ-регуляторов. Наиболее часто используемая схема изображена на рис.3.4, а. Она представляет собой последовательное соединение усилительного и интегрирующего звеньев, причем первое охвачено отрицательной обратной связью с апериодическим звеном. По такой структурной схеме выполнены регуляторы электронной агрегатной унифицированной системы. Передаточная функция такого регулятора имеет следующий вид:

где k_p=Т_И/δ_рТ_ИМ; s=1/k₁δ_ρ=T_имk_р/Т_иk₁·Обозначим через k_δ=l/(s+1) и Т_б=sТ_и/(s+1).

С учетом этих обозначений получим передаточную функцию балластного звена в виде:

W_б(р)=k_б/(T_бр+1)

В этом случае балластное звено представляет собой апериодическое звено с коэффициентом усиления k₆ и постоянной времени.

Рис.3.4. Структурная схема и переходные характеристики реального линейного ПИ-регулятора

Для данной структурной схемы коэффициент усиления регулятора зависит от постоянной времени Т_ИМ интегрирующего звена, т.е. от времени полного хода исполнительного механизма. Известно, что постоянная времени исполнительного механизма в свою очередь зависит от нагрузки, поэтому от нагрузки зависит и k_p. В таких регуляторах наблюдается взаимосвязь обоих настроечных параметров - коэффициента усиления k_p и времени интегрирования Т_и.

Переходные характеристики регулятора со структурной схемой, изображенной на рис. 3.4, а, приведены на рис.3.4, б.

Видно, что при s=0 регулятор становится идеальным. Чем больше значение s, тем сильнее отклонение характеристики реального регулятора от характеристики идеального.

3. ПИД-регуляторы. Эти регуляторы также могут быть построены по различным структурным схемам. Одна из типичных структурных схем изображена на рис.3.5, а. Она позволяет строить ПИД-регуляторы из унифицированных блоков. Для формирования, пропорционально-интегральной составляющей сигнала регулирования используется блок, схема которого показана на рис.3.5, а. Дифференцирующий блок 1 конструктивно может выполняться отдельно от других блоков.

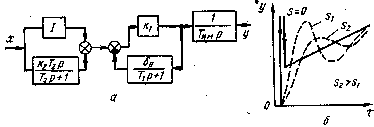
Рис.3.5. Структурная схема и переходные характеристики реального линейного ПИД-регулятора

Передаточная функция регулятора с такой структурной схемой может быть записана в виде:

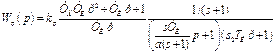
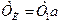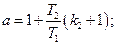
где ; 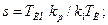s₂=T₂/T_И

В этом случае передаточная функция балластного звена имеет вид:

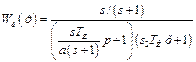
Это - передаточная функция апериодического звена второго порядка. Максимальное отношение Т_Д/Т_И =0,25. Оно достигается при а=2 или (T_2/T₁) (k₂ + 1)=1. Это обстоятельство может рассматриваться как недостаток подобных схем, поскольку ограничивает область применения ПИД-регуляторов. Переходные характеристики регуляторов приведены на рис.3.5, б. При регулятор становится идеальным.