Косозубые и шевронные колеса
Диаметр окружности впадин
Диаметр окружности выступов
da=d+2m=m (z+2),(77.12)
df = d - 2,5 m=m (z-2,5), (7.13)
Толщина зуба и ширина впадины по делительной окружности равны
между собой
P = St +Lt , (7.14)
где, St – толщина зуба;
Lt – ширина впадин.
Межцентровое расстояние двух сцепляющихся зубчатых колес определя-ется по формуле
aω= m (z1+z2 ) / 2, (7.15)
Путь, проходимый профилем зуба по начальной (делительной) окружности за время фактического его зацепления называется дугой зацепления S.
Необходимым условием непрерывности зацепления является требование, чтобы дуга зацепления была больше шага зацепления, т.е.:
S >р.
Отношение длины дуги зацепления к шагу зацепления называется коэффициентом перекрытия:
ε = S / р,(7.16)
Коэффициент перекрытия характеризует среднее число пар зубьев, одновременно находящихся в зацеплении. Для цилиндрических передач принимают ε> 1,2.
Цилиндрические колеса, у которых зубья расположены по винтовой линии на делительном цилиндре, называют косозубыми. В отличие от прямозубых передач в косозубой передаче зубья входят в зацепление не сразу по всей длине, а постепенно, что снижает шум и динамические нагрузки. Чем больше угол наклона линии зуба β, тем выше плавность зацепления. (рисунок 7.6).
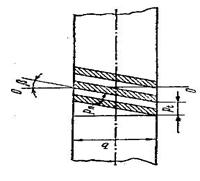
Рисунок 7.6 – Развертка обода косозубого колеса
В косозубом колесе шаг измеряют в окружном (pt) либо в нормальном (Рn) направлении. Соответственно и модуль бывает окружным и нормальным.
mt= pt / π, mn= pn / π,(7.17)
т.к. Pt=Pn/cos β, то mt= mn/ cos β,(7.18)
С учетом этого все параметры зубчатого колеса, в которые входит модуль, рассчитываются с использованием окружного модуля:
- делительный диаметр
d= mt∙z=( mn∙z)/( cos β), (7.19)
- диаметр окружности вершин зубьев
da= mt ∙z+2m=mn((z/ cos β)-2), (7.20)
- диаметр окружности впадин
df= mt∙z-2,5m= mn((z/ cos β)-2,5), (7.21)
- межосевое (межцентровое) расстояние
aω= mt(z1+z2)/2= mn(z1+z2)/2cosβ, (7.22)
Прямозубую передачу можно рассматривать как косозубую, у которой
β=0, и mn= mt, (7.23)