Проверка
Глава 2. Системы линейных алгебраических уравнений
Пусть дано n неизвестных x1, x2, xi, … , xn. Система m линейных уравнений с n неизвестными xi, 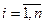 , имеет вид
, имеет вид
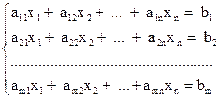 (2.1)
(2.1)
здесь аij коэффициенты при неизвестных, причем i – номер уравнения, а j – номер неизвестного. Величины bi - свободные члены. В в матричной форме систему можно записать так
AּX = B, (2.2)
где 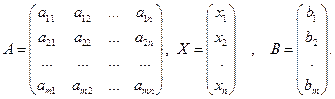
Матрица A, составленная из коэффициентов при неизвестных, называется основной (базовой) матрицей системы, X - матрица-столбец неизвестных, B - матрица-столбец свободных членов. Если к основной матрице системы приписать столбец свободных членов, то получится расширеннаяматрица системы уравнений
 (2.3)
(2.3)
Если все свободные члены равны нулю, то система называетсяоднородной, в противном случае система неоднородна. Линейные системы, полученные одна из другой путем элементарных преобразований (перестановкой двух уравнений, умножением одного из них на число, не равное нулю, почленным сложением двух уравнения) называютсяэквивалентными(или равносильными). Все эквивалентные системы имеют одинаковые решения.
Решение системы линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:
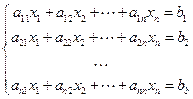 (2.4) (2.4)
| ||||
Вычислим определитель системы 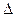
| ||||
 (2.5) (2.5)
| ||||
Если 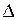 ¹0, то система (2.4) имеет решение, и при том единственное. Если
¹0, то система (2.4) имеет решение, и при том единственное. Если 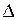 = 0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
= 0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
В дальнейшем мы будем предполагать, что 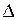 ¹0.
¹0.
1. Решение с помощью формул Крамера.
Если определитель системы 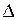 ¹0, то, согласно формулам Крамера, решение системы (2.4) можно представить в виде
¹0, то, согласно формулам Крамера, решение системы (2.4) можно представить в виде
 (2.6) (2.6)
|
Здесь
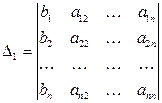 ; ;
|  ; ;
| ||
 . .
| |||
Определитель  (i=1, 2,…, n) отличается от определителя системы
(i=1, 2,…, n) отличается от определителя системы 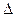 тем, что
тем, что  столбец
столбец 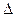 заменен столбцом из свободных членов, т.е. столбец
заменен столбцом из свободных членов, т.е. столбец 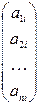 заменен на столбец
заменен на столбец  .
.
Пример. Дана расширенная матрица системы  . Решить систему методом Крамера.
. Решить систему методом Крамера.
Решение. Запишем систему в стандартной форме
 .
.
Определитель данной системы


Вычислим определители  ,
,  и
и  :
:

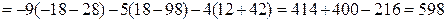 .
.

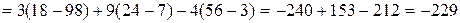 .
.

 .
.
Решение системы: 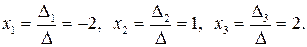
Для того чтобы убедиться в правильности решения, подставим эти значения 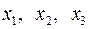 в исходную систему
в исходную систему
 .
.
2. Решение методом Гаусса. Пусть есть система (2.4) с определителем 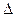 ¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
 . .
|
Метод Гаусса состоит в том, что система (2.4) с помощью ряда элементарных преобразований сводится к новой системе, расширенная матрица которой имеет вид
 . (2.7) . (2.7)
|
Т.е. в результате преобразований все коэффициенты матрицы 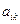 становятся равными нулю, кроме диагональных элементов, которые становятся равными единице:
становятся равными нулю, кроме диагональных элементов, которые становятся равными единице: 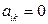 при
при 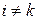 и
и 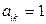 при
при  . Столбец свободных членов
. Столбец свободных членов  превращается в новый столбец
превращается в новый столбец 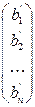 .
.
Если мы привели нашу матрицу к диагональному виду, то решение системы записывается очень просто:
 (2.8) (2.8)
|
Таким образом, решение системы сводится к совершению элементарных преобразований, в результате которых расширенная матрица (5) превращается в расширенную матрицу (6).
К элементарным преобразованиям системы (1) относятся следующие:
1) перемена местами уравнений (т.е. перемена местами строк расширенной матрицы);
2) умножение или деление любого уравнения системы (1) на число, отличное от 0 (т.е. умножение или деление строки расширенной матрицы на число, отличное от 0);
3) изменение любого уравнения системы (1) путем прибавления к нему другого уравнения системы, умноженного на число, отличное от 0 (т.е. изменение строки расширенной матрицы путем прибавления к ней другой строки, умноженной на число, отличное от 0).
Пример. Найти решение системы методом Гаусса.
 .
.
Решение.Определитель системы  . Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
. Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
 .
.
Далее мы будем приводить нашу матрицу к диагональному виду и выписывать ее вид после каждого шага преобразований.
1-й шаг. Разделим 1-ю строку матрицы на 2.
 .
.
2-й шаг. 1-ю строку оставляем без изменения. Вместо 2-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-5), складываем ее со 2-й строкой, тогда новые числа, стоящие во 2-й строке расширенной матрицы, будут следующие:


Вместо 3-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-3) и складываем ее с 3-й строкой, тогда


Расширенная матрица примет вид
 .
.
В результате первых 2-х шагов 1-й столбец  преобразовался в
преобразовался в  .
.
3-й шаг. Делим вторую строку на 11.
 .
.
4-й шаг. 2-ю строку оставляем без изменения. Вместо 1-й строки записываем следующую ее комбинацию со 2-й: 2-ю строку умножаем на 2 и складываем ее с 1-й строкой, тогда

Вместо 3-й строки записываем ее комбинацию со 2-й: 2-ю строку умножаем на (-14) и складываем ее с 3-й строкой, тогда


 .
.
В результате 3-го и 4-го шагов 1-й столбец матрицы не изменился, а 2-й превратился в  .
.
5-й шаг. Делим 3-ю строку на 
 .
.
6-й шаг. 3-ю строку оставляем без изменения. Вместо 1-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на  и складываем ее с 1-й строкой, тогда
и складываем ее с 1-й строкой, тогда


Вместо 2-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на  и складываем ее со 2-й строкой, тогда
и складываем ее со 2-й строкой, тогда


 .
.
В результате 5-го и 6-го шагов 3-й столбец принял вид  .
.
Таким образом, решение системы следующее: 

Таким образом, смысл метода Гаусса состоит в том, что сначала 1-й столбец исходной матрицы приводим к виду  , затем 2-й - к виду
, затем 2-й - к виду  и, наконец, 3-й – к виду
и, наконец, 3-й – к виду  . При этом происходит преобразование столбца свободных членов.
. При этом происходит преобразование столбца свободных членов.