Пример.
Пример.
.
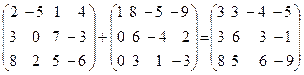Умножение матрицы на число. Произведением матрицы A=(aik)m,n на число a называется матрица C=(cij)m,n, элементы которой получаются из соответствующих элементов матрицы A умножением на число a:
C = a A, где cij = a×aij. (1.11)
.
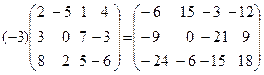Операции сложения матриц и умножения число называются линейными операциями. Эти операции обладают следующими свойствами:
A + B = B + A (перестановочный закон);
(A + B) + C = A + (B + C) (сочетательный закон);
(a+b)A=aA+bA (распределительный закон);
(A + B) = A + B;
A + (-A) = 0
A + 0 = A,
где A, B, C, 0 матрицы одного размера, a, b - числа.
Замечание. Пусть A, B - квадратные матрицы порядка n > 1. Линейные операции над матрицами не переносятся на их определители, т.е. det(A+B) ¹ detA + detB, det(aּA) ¹ aּdetA, но det(aA)=an ּdetA.
Произведение матриц. Произведение матриц AmkּBkn = Ckn определено только в том случае, если число столбцов матрицы A равно числу строк матрицы B, при этом матрица С имеет размер mּn. Элементы матрицы С определяются по формуле
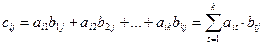(1.12)
Умножение матриц производится по правилу "строка на столбец".
Произведение матриц не перестановочно, в общем случае AּB BּA.
Пример. Найти произведения матриц A =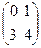 
и B =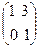 
.
Поскольку это квадратные матрицы одного размера, то умножение таких матриц возможно, причем существует и АВ и ВА. В соответствии с (2.2) имеем:
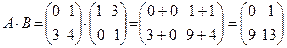
Свойства операции умножение матриц:
1) Aּ (BּC) = (AּB) ּС;
2) aּ (AּB) = (aּA) ּB = Aּ (aּB);
3) (A+B) ּC = AּC + BּC;
4) Cּ (A+B) = CּA + CּB,
где a - число, A, B, C матрицы, для которых произведения cуществуют;
5) если A, B - квадратные матрицы одного порядка, то
det (AּB) = detA ּ detB.
Транспонирование матриц. Рассмотрим произвольную матрицу
.
Матрица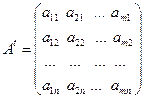 
полученная из матрицы A заменой строк столбцами, называется транспонированнойпо отношению к A.
Например,если A =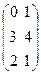 
, то At = 
.
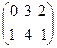Свойства операции транспонирования матриц
1) (At)t = A;
2) (A + B)t= At+ Bt;
3) (aּA)t= aAt:
4) (AּB)t = BtּAt,
(AּB)t = BtּAt, где A и B - матрицы, a- число;
5) Если A- квадратная матрица, то detA=detAt.