Задачи линейного программирования. Симплекс-метод.

Система линейных неравенств и область их решения. Пусть задано линейное неравенство с двумя переменными х₁ и х₂:

a₁x₁₊a₂x₂+b≥0. (20.1)

Если величины х₁ и х₂ рассматривать как координаты точки плоскости, то совокупность точек плоскости, координаты которых удовлетворяют неравенству (20.1), называется областью решений данного неравенства. Областью решений неравенства (20.1) является полуплоскость.

Для того чтобы установить, какая из двух полуплоскостей соответствует неравенству (20.1), достаточно привести это неравенство к виду x₂≥kx₁+l или к виду х₂≤kx₁+l. В первом случае искомая полуплоскость лежит выше прямой а₁х₁+а₂ x₂+b= 0, во втором — ниже ее. Если же а₂=0, то неравенство приводится к одному из видов x₁≥h или x₁≤h, т. е. полуплоскость лежит справа или слева от прямой x₁= h.

В случае же, когда задана система неравенств

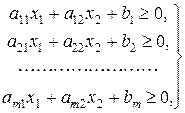(20.2)

где т — конечное число, получим пересечение конечного числа полуплоскостей, образующее многоугольную область D. Область D называется областью решений системы неравенств (20.2) Эта область не всегда бывает ограничена, она может быть и неограниченной и даже пустой. Последний случай имеет место тогда, когда система неравенств (20.2) противоречива. Могут быть также случаи лишних неравенств, входящих в совместную систему и определяющих прямые, не имеющие с областью D общих точек. Такие неравенства можно исключить.

Область решений обладает важным свойством — она является выпуклой, т. е. вместе с любыми своими двумя точками содержит и весь соединяющий их отрезок Прямая, которая имеет с областью по крайней мере одну общую точку, притом так, что вся область лежит по одну сторону от этой прямой, называется опорной по отношению к этой области.

Аналогично истолковывается геометрически и система неравенств с тремя переменными

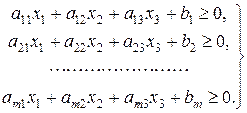(20.3)

Здесь каждое из неравенств выполняется для одного из полупространств, на которые разбивает все пространство соответствующая плоскость Система неравенств (20.3) представляет собой пересечение полупространств, т. е. многогранную область решений системы неравенств.

Основная задача линейного программирования. Графическое решение. Задача линейного программирования заключается в изучении способов отыскания наибольшего или наименьшего значений линейной функции при наличии линейных ограничений.

Функция, наибольшее или наименьшее значение которой отыскивается, называется целевой функцией, а совокупность значений переменных, при которых достигается наибольшее или наименьшее значение, определяет так называемый оптимальный план. Всякая же другая совокупность значений, удовлетворяющая ограничениям, определяет допустимый план (решение).

Пусть ограничения заданы совместной системой т линейных неравенств с п переменными:

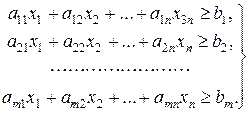
Среди неотрицательных решений этой системы требуется найти такое решение, при котором линейная функция (целевая функция)

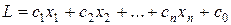
принимает наибольшее (наименьшее) значение или, как говорят, максимизировать (минимизировать) линейную форму L.

Покажем, как решается указанная задача геометрическим методом, для чего ограничимся рассмотрением совместной системы линейных неравенств с двумя и тремя переменными. Пусть, кроме того, задана линейная функция L=c₁x₁+c₂x₂+c₀. Найдем среди множества точек (x₁; х₂) из области решений совместной системы неравенств такие, которые придают заданной линейной функции наименьшее (наибольшее) значение. Для каждой точки плоскости функция L принимает фиксированное значение L=L₁. Множество всех таких точек есть прямая c₁x₁+c₂x₂+c₀=L₁ перпендикулярная вектору C(c₁, с₂), выходящему из начала координат. Если эту прямую передвигать параллельно самой себе в положительном направлении вектора С, то линейная функция L = c₁x₁ +c₂x₂ + с₀ будет возрастать, а в противоположном направлении — убывать. Пусть при движении прямой L в положительном направлении вектора С она впервые встретится с многоугольником решений в его вершине, тогда в этом положении L₁ прямая L становится опорной, и на этой прямой функция L принимает наименьшее значение. При дальнейшем движении в том же направлении (положительном) прямая L пройдет через другую вершину многоугольника решений, выходя из области решений, и станет также опорной прямой L₂; на ней функция L принимает наибольшее значение среди всех значений, принимаемых на многоугольнике решений.

Таким образом, минимизация и максимизация линейной функции L=c₁x₁+c₂x₂+c₀ на многоугольнике решений достигаются в точках пересечения этого многоугольника с опорными прямыми, перпендикулярными вектору С(с₁,с₂). Опорная прямая может иметь с многоугольником решений либо одну общую точку (вершину многоугольника), либо бесконечное множество точек (это множество есть сторона многоугольника).

Аналогично, линейная функция трех переменных L=c₁x₁+c₂x₂+c₃x₃+c₀ принимает постоянное значение из плоскости, перпендикулярной вектору С(с₁;с₂;с₃). Наименьшее и наибольшее значения этой функции на многограннике решений достигаются в точках пересечения этого многогранника с опорными плоскостями, перпендикулярными вектору С(с₁; с₂; с₃). Опорная плоскость может иметь с многогранником решений либо одну общую точку (вершину многогранника), либо бесконечное множество точек (это множество есть ребро или грань многогранника).

Пример 20.1. Максимизировать линейную форму L=2х₁+2х₂ при ограничениях:

Зх₁ -2х₂ ≥- 6, 3х₁ +х₂≥З, x₁≤3.

Заменив знаки неравенств на знаки точных равенств, построим область решений по уравнениям прямых Зx₁—2x₂ + 6 = 0, Зх₁ +х₂—3 = 0, х₁=3 (рис. 15).

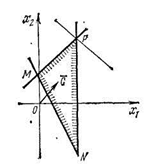
Рис. 15

Областью решений неравенств является треугольник MNP. Построим вектор С(2; 2). Тогда опорная прямая при выходе из треугольника решений пройдет через точку Р(3; 15/2), а потому в точке Р линейная функция L=2х₁ + 2х₂ принимает наибольшее значение, т. е. максимизируется, и L_max=2∙3+ 2∙(15/2)=21.

Симплекс-метод.Решение основной задачи линейного программирования геометрическим методом является наглядным в случае двух и даже трех переменных. Для случая же большего числа переменных геометрический метод становится невозможным. Так называемый симплекс-метод принадлежит к числу аналитических методов решения основной задачи линейного пpoграммирования. Система ограничений в вычислительных методах обычно задается системой линейных уравнений

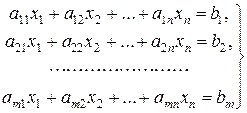(20.4)

и среди неотрицательных решений системы уравнений (20.4) надо найти такие, которые максимизировали бы линейную функцию

.

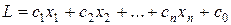Выразим 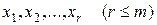через остальные переменные:

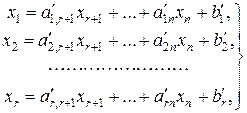(20.5)

где 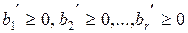. Если ограничительные условия заданы неравенствами, то их можно преобразовать в равенства путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих). Например, в неравенстве a₁x₁+…+ а_пх_п≤ b достаточно добавить к левой части некоторую величину x_n+1 ≥0, получится равенство

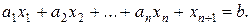
Ограничительные условия могут задаваться и смешанным образом, т. е. неравенствами и уравнениями, тогда указанным путем их можно свести только к уравнениям. Переменные (неизвестные) х₁ х₂,...,х_r называются базисными, а весь набор {х_1; х₂, ..., х_r} — базисом, остальные переменные называются свободными, система ограничений (20.5) называется системой, приведенной к единичному базису. Подставляя в линейную форму L вместо базисных переменных их выражения через свободные из системы (20.5), получим

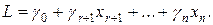
Теперь, полагая все свободные переменные равными нулю, найдем значения базисных переменных: 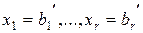. Таким образом, решение 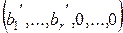системы является допустимым — оно называется базисным. Для полученного базисного решения значение линейной формы L_Б = у₀. Решение задачи с помощью симплекс-метода распадается на ряд шагов, заключающихся в том, что от данного базиса Б мы переходим к другому базису Б' с таким расчетом, чтобы значение L_Б уменьшалось или, по крайней мере, не увеличивалось, т. е. .

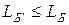Пример 20.2. Максимизировать линейную форму L=-х₄+х₅ при ограничениях: x₁ +x₄—2x₅=1, х₂ — 2х₄ + x₅ = 2, х₃ +Зx₄ + х₅ = 3.

Данная система уравнений-ограничений совместна, так как ранги матрицы системы

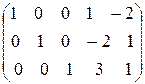
и расширенной матрицы

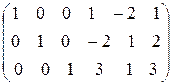
совпадают и равны 3. Следовательно, система уравнений совместна и три переменные (базисные) можно линейно выразить через две свободные переменные. Выразим, например х₁, х₂ и х₃ через х₄ и х₅, т. е. приведем систему к единичному базису:

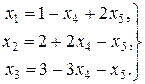
Линейную форму L = — х₄ +х₅ выразим через свободные переменные x₄ и х₅ (в данном примере L уже выражена через х₄ и х₅). Теперь при х₄ = 0, х₅ = 0 найдем значения базисных переменных: x₁=1, x₂ = 2, х₃ = 3. Таким образом, первое допустимое решение системы уравнений есть х₁=1, х₂ = 2, x₃, = 3, x₄ = 0, х₅=0, или (1, 2, 3, 0, 0). При найденном допустимом решении линейная форма L имеет значение 0, т. е. L₁ = 0.

Теперь попытаемся увеличить значение L₁, увеличение х₄ уменьшит L₁, так как перед х₄ стоит отрицательный коэффициент, а увеличение х₅ даст увеличение и L₁. Увеличим поэтому х₅ так, чтобы x₁, х₂, х₃ не стали отрицательными, оставив х₄ = 0. Из второго уравнения системы следует, что х₅, можно увеличить до 2. Таким образом, получаем следующие значения переменных x₁=5, х₂ = 0, x_з=1. x₄=0, x₅ = 2 или (5, 0, 1, 0, 2).

Значение линейной формы L при этом допустимом решении равно L₂ = 2, т. е. при втором шаге оно увеличилось.

Далее, примем за свободные переменные х₂ и х₄ т. о., именно те переменные, которые в новом решении имеют нулевые значения С этой целью из второго уравнения системы выразим х₅ через х₂ и х₄ и получим х₅ = 2—х₂ +2х₄.

Тогда

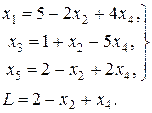
Для увеличения значения L будем увеличивать x₄. Из второго уравнения последней системы видно, что при условии неотрицательности x₃ значение x₄ можно довести до x₄ =1/5. При этом условии новое допустимое решение есть х₁=8/5, x₂ = 0, x₃ = 0, х₄=1/5, x₅=12/5 или (28/5, 0, 0, 1/5, 12/5). Значение линейной формы при этом L₃= 11/5.

Выразим теперь х₁, x₄, х₅ через свободные переменные x₂ и x₃:

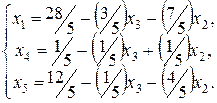
Так как в последней линейной форме обе свободные переменные входят с отрицательными коэффициентами, то наибольшее значение L достигается при x₂=0, x_з = 0. Это означает, что решение (28/5, 0, 0, 1/5, 12/5) является оптимальным и L_max = ll/5.