ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ МОСТИКОМ УИТСТОНА

Алтайский государственный технический университет им. И.И. Ползунова

Кафедра физики

 

 

ОТЧЕТ

ПО ЛАБОРАТОРНОЙ РАБОТЕ ПО ФИЗИКЕ

 

 

 

 

Студент ________________________ Группа ________________________ Факультет ______________________ Преподаватель ___________________

 

 

Барнаул - 2015

ЛАБОРАТОРНАЯ РАБОТА № 24

ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ МОСТИКОМ УИТСТОНА

Цель работы:ознакомиться с принципом работы схемы мостика Уитстона. Определить неизвестное сопротивление и удельное сопротивление проводника.

Рис. 2.Схема мостика Уитстона

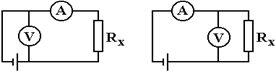а) б) Рис. 1.Схема определения сопротивления

Теоретическое введение.Наиболее часто для измерения сопротивления проводника применяется одна из схем, приведенных на рис. 1 (а и б), в силу их простоты. Однако любая из этих схем обладает существенным недостатком. В самом деле, любой прибор обладает конечным, но не нулевым сопротивлением. Поэтому, даже при высоком классе точности приборов, вольтметр, в первом случае, будет показывать суммарное падение напряжения на амперметре и исследуемом сопротивлении (показания амперметра соответствуют току через R_Х). Во втором случае амперметр будет показывать суммарный ток, протекающий через вольтметр и сопротивление R_Х. Показания же вольтметра соответствуют падению напряжения на R_Х. Таким образом, в любом из этих случаев значение сопротивления R_Х, найденное из закона Ома, будет неверным.

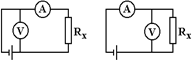а) б) Рис. 1.Схема определения сопротивления.

Рис. 2.Схема мостика Уитсона.

Схема, сводящая к минимуму влияние прибора на точность измерений, была предложена Уитстоном - так называемый мостик Уитстона (рис. 2). Четыре сопротивления R₁, R₂, R₃, R₄ образуют плечи мостика. R_Б и e - сопротивление и ЭДС батареи. R_г и I_г - сопротивление гальванометра и ток, протекающий через него.

Для расчета сложных цепей, одной из которых является мостик Уитстона, применимы правила Кирхгофа.

Первое правило: алгебраическая сумма токов, сходящихся в любой точке разветвленной цепи, равна нулю:

(1).

Токи учитываются со знаком «+», если они приходят в рассматриваемую точку, и со знаком «–», если они выходят из этой точки. Первое правило Кирхгофа применяется к узловым точкам цепи, в которых сходятся три и более токов. Первое правило вытекает из закона сохранения электрического заряда.

Второе правило: если несколько участков электрической цепи образуют замкнутый контур, то сумма падений напряжений на всех участках этого контура равна сумме ЭДС, действующих в этом контуре:

(2).

Падение напряжения I×R считается положительным, если выбранное направление тока на данном участке контура совпадает с направлением обхода контура и отрицательным, если направление тока и обхода противоположны. ЭДС e имеет положительное значение, если при обходе контура внутри элемента переходим от «–» полюса источника к «+», и отрицательное, если наоборот.

Воспользовавшись правилами Кирхгофа, можно получить шесть независимых уравнений для мостика Уитстона. По первому правилу Кирхгофа для узлов А, В и С:

(3)

По второму правилу Кирхгофа для контуров АВСeА, АВDА и ВСDВ

(4) .

Эти уравнения позволяют найти шесть неизвестных величин. Если неизвестно одно из сопротивлений, например R₁, то измеряя гальванометром силу тока I_г, из уравнений получают остальные токи и искомое сопротивление R₁. Так поступают в случае неравновесного мостика Уитстона. Изменяя сопротивления R₂, R₃, R₄, можно добиться, что ток через гальванометр станет равным нулю. В этом случае гальванометр не внесет искажений в схему, и уравнения (3) примут вид

I₁ = I₂ I₃ = I₄,

из уравнений (4) получим:

I₁×R₁ = I₃×R₃ I₂×R₂ = I₄×R₄ ,

отсюда: 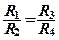(5) .

Неизвестное сопротивление R₁ можно выразить через три других сопротивления

(6) .

Равенство нулю силы тока через гальванометр определяет равновесное состояние мостика Уитстона. В этом случае, как видно из формулы (6), для вычисления неизвестного сопротивления необходимо знать абсолютное значение сопротивления R₂ и отношение R₃/R₄.