Теорема о равенстве смешанных производных

П.1. Производные высших порядков.

Геометрический смысл первого дифференциала

Производные и дифференциалы высших порядков.

Дифференцируемость функции многих переменных.

Лекция 3

Геометрические приложения частных производных.

Пусть дана дифференцируемая функция n переменных u(. Пусть также вычислена производная первого порядка по переменной , непрерывна в точке .

Пусть . Тогда .

Рассмотрим выражение, аналогичное предложенному выше:

,

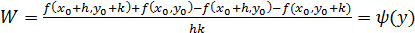где

 

.

Аналогично получаем, что при выполнено .

Следовательно,

.

▲

Справедлива следующая общая теорема.

Теорема ( без доказательства).

Пусть функция определена в области . Пусть существуют и непрерывны все частные производные до k -го порядка включительно в области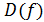. Тогда смешанные производные до -го порядка не зависят от порядка дифференцирования.

Пример. Рассмотрим функцию двух переменных, у которой смешанные производные второго порядка существуют, но не равны в точке (0,0):

Имеем:

Видим, что