Необходимые теоремы и опорные задачи для окружности, вписанной в треугольник и четырехугольник, и окружности, описанной около треугольника и четырехугольника.
Приложение 1
| 1. Вписанная окружность – ее центр и радиус. | ||

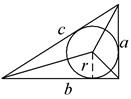
| O – точка пересечения биссектрис углов ∆ABC,
r – радиус вписанной окружности,
S – площадь ∆ABC
 - для любого ∆ - для любого ∆
| Центр вписанной окружности находится в точке пересечения биссектрис углов треугольника. |
| 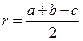 -
- для прямоугольного ∆,
где c - гипотенуза -
- для прямоугольного ∆,
где c - гипотенуза
| Центр вписанной окружности находится в точке пересечения биссектрис углов треугольника. |

| 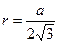 -
- для правильного ∆,
где a - сторона -
- для правильного ∆,
где a - сторона
| Центр вписанной окружности находится в точке пересечения биссектрис углов треугольника, медиан и высот. |
| 2. Описанная окружность – ее центр и радиус. | ||

| O – точка пересечения серединных перпендикуляров,
R – радиус описанной окружности
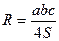 - для любого ∆, - для любого ∆,

| Центр описанной окружности находится в точке пересечения серединных перпендикуляров |
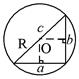
| 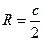 - для прямоугольного ∆, где с – гипотенуза - для прямоугольного ∆, где с – гипотенуза
| Центр описанной окружности находится в точке пересечения серединных перпендикуляров, делит гипотенузу пополам. |
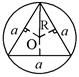
| 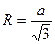 - для правильного ∆,
где а - сторона - для правильного ∆,
где а - сторона
| Центр описанной окружности находится в точке пересечения серединных перпендикуляров, биссектрис, медиан. |
| 3.Окружность. Касательные. Секущие. Хорды. Углы. | ||||

| AO∙OB = CO∙OD, где O – точка пересечения хорд AB и CD | Произведение отрезков одной хорды равно произведению отрезков другой хорды относительно точки их пересечения. | ||
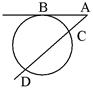
| AB2 = AC∙AD, где AB – касательная, B – точка касания | Произведение отрезка секущей на ее внешнюю часть равно квадрату отрезка касательной, проведенных к окружности из одной точки. | ||

| AB∙AC = AD∙AK, где AC и AK - секущие | Произведение отрезка секущей на ее внешнюю часть есть величина постоянная. | ||

| AB – касательная,
BC – хорда

| Угол, образованный касательной и хордой, проведенных к окружности из одной точки, измеряется половиной дуги, заключенной внутри сторон этого угла. | ||
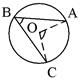
|  - вписанный угол, - вписанный угол,
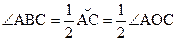
| Вписанный угол измеряется половиной дуги, на которую он опирается и равен половине центрального угла, опирающегося на ту же дугу. | ||

| AB, CD – хорды
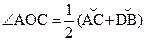
| Угол, вершина которого находится внутри окружности, измеряется полусуммой дуг, заключенных внутри сторон угла. | ||
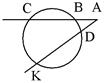
| AC и AK – секущие,
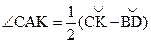
| Угол, образованный двумя секущими, измеряется полуразностью дуг, заключенных внутри сторон этого угла. | ||
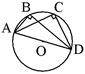
| AD – диаметр окружности,
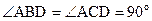
| Вписанный угол, который опирается на диаметр, равен 90о. | ||
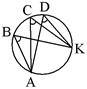
| 
| Вписанные углы, которые опираются на одну и ту же дугу, равны между собой. |
| 4. Теорема об отрезках касательных | |||
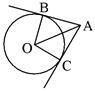
| АВ = АС – касательные,
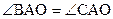
| Отрезки касательных равны. АО – биссектриса угла ВАС | |
| 5. Пропорциональные отрезки в прямоугольном треугольнике. | |||
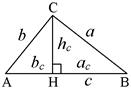
| 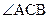 - прямой,
∆AHC, ∆CHB, ∆ACB –
подобны между собой - прямой,
∆AHC, ∆CHB, ∆ACB –
подобны между собой
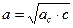 , , 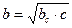

| Высота, проведенная из вершины прямого угла на гипотенузу, делит данный ∆ на 2 подобных и каждый из них подобен данному. Каждый катет есть среднее пропорциональное (среднее геометрическое) между гипотенузой и проекцией катета на гипотенузу. Высота, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу. | |
| 6. Вписанный и описанный четырехугольники. | |||

| 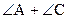 = 180o, = 180o,
 = 180o = 180o
| Если суммы противоположных углов четырехугольника равны 180о, то около него можно описать окружность. Верна и обратная теорема. | |
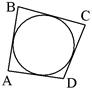
| AB + CD = AD + BC | Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. Верна и обратная теорема. | |