Построение опорного плана транспортной задачи
Его можно найти несколькими способами. Рассмотрим наиболее распространенные.
а) Метод северо-западного угла.
Он заключается в том, что в начале максимально допустимое количество груза помещается в верхнюю левую (северо-западную) клетку таблицы, затем заполняется соседняя клетка в строке или в столбце, в зависимости от того, где имеются еще неиспользованные возможности перевозок.
Таким же образом (вправо и вниз) производится распределение всего количества груза.
При таком заполнении стоимость перевозки единицы груза не учитывается.
Пример.
Построить опорный план транспортной задачи для исходных данных, приведенных в таблице.
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Определим тип задачи

140+180+160=480

 следовательно, задача закрытого типа. Построим опорный план методом северо-западного угла .
следовательно, задача закрытого типа. Построим опорный план методом северо-западного угла .
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Таким образом , опорный план имеет вид:

Определим стоимость перевозок:
С0=2×60+3×70+4×10+1×110+7×60+2×100=1380
б) Метод минимального элемента.
В этом случае на каждом шаге вычислений выбирают клетку с минимальным тарифом перевозок (если таких клеток несколько , то выбирают любую из них) и помещают в эту клетку максимально допустимое количество груза, с учетом имеющихся запасов и требуемых потребностей. Заполняя по этому принципу требуемое количество клеток, получим опорный план; при этом стоимость перевозок, как правило, меньше, чем в предыдущем методе.
Пример:
Построить опорный план транспортной задачи для условий предыдущего примера методом минимального элемента.
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
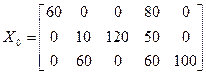
С0=2×60+2×80+4×10+120+4×50+7×60+2×100=1260