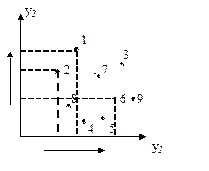Графический способ построения множества Парето
Алгоритм формирования множества Парето
Пусть имеется n альтернатив, каждая из которых характеризуется набором частных критериев. Алгоритм состоит из n циклов сравнения каждой альтернативы с уже вошедшими в множество Парето
В каждом цикле сравнения возможны три исхода:
Если сравниваемая альтернатива по всем частным критериям хуже чем хотя бы одна из вошедших в множество Парето, то альтернатива исключается из рассмотрения.
Если сравниваемая альтернатива хотя бы по одному частному критерию хуже, а по другим лучше, чем каждая из альтернатив уже вошедших в множество Парето, то эта альтернатива добавляется в множество Парето.
Пример Пусть имеется 9 альтернатив, каждая из которых характеризуется двумя «хорошими» частными критериями у1 и у2. Процесс построения множества Парето по описанному выше алгоритму отображается следующей таблицей
| Альтернативы | y1,y2 | Циклы сравнения | Множество Парето | Пояснения |
| 3, 10 | Первая альтернатива входит в состав множества Парето автоматически. | |||
| 2, 9 | А2 не включена в Парето, так как хуже А1 по обоим критериям | |||
| 9, 5 | 1, 3 | А3 добавлена в Парето, так как лучше А1 по у1, но хуже по у2 | ||
| 6, 7 | 1, 3, 4 | А4 добавлена в Парето, так как не хуже и не лучще А1 и А3 | ||
| 4, 4 | 1, 3, 4 | А5 не включена в Парето, так как хуже А3 и А4 по обоим критериям | ||
| 6, 4 | 1, 3, 4 | А6 не включена в Парето, так как хуже А3 по обоим критериям | ||
| 8, 3 | 1, 3, 4 | А7 не включена в Парето, так как хуже А3 по обоим критериям | ||
| 7, 8 | 1, 3, 8 | А8 включена в Парето, так как не хуже и не лучще А1 и А3. А4 исключена из Парето, так как хуже А8 по обоим критериям | ||
| 10, 6 | 1, 8, 9 | А9 включена в Парето, так как не хуже и не лучще А1 и А8. А3 исключена из Парето, так как хуже А9 по обоим критериям |
Важно заметить, что описанный алгоритм построения множества Парето применим только для сформулированного условия компромисса – альтернативы равноценны, если хотя бы по одному частному критерию одна лучше другой. Для других условий компромисса алгоритмы построения множества Парето будут другими.
Множество Парето для двух критериев можно построить графически. Для каждой альтернативы, представленной на графике точкой, строится прямоугольник. На рисунке такие прямоугольники построены для точек 1, 2 и 6. Очевидно, угловая точка каждого прямоугольника является лучшей точкой по отношению ко всем другим, оказавшимся внутри этого прямоугольника, так как у этой угловой точки значения критериев у1 и у2 наибольшие. Поэтому все точки, оказавшиеся внутри построенных прямоугольников, например, точки 8, 4, 5 для прямоугольника с вершиной в точке 6 и точка 2 для прямоугольника с вершиной в точке 1, исключаются из рассмотрения. Процесс продолжается до тех пор, пока не будут построены прямоугольники для всех точек. Неисключенные точки (в данном случае это точки 1, 3, 9) образуют множество Парето. Заметим, что при других направлениях улучшения критериев y1, y2 правила построения прямоугольников (точнее, углов) и исключения точек будут другими. Например, на приведенном ниже рисунке лучшей будет угловая точка угла 1, а угловые точки для углов 2 и 3 будут исключены.