Нормирование частных критериев.

Если частные критерии yi имеют разные размерности, то их нужно приводить к безразмерным величинам, иначе их суммирование бессмысленно (нельзя складывать килограммы и рубли). Приведение всех частных критериев к одной размерности или безразмерной величине называется нормированием. Оно выполняется делением нормируемой величины на некоторую заданную величину, называемую нормирующим множителем, имеющим ту же размерность, что и нормируемая величина.

Примеры:

a) где y_{i заданное} — значение частного i - го критерия, заданное заказчиком.

b) 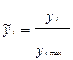, где y_{i_max} — максимальное достижимое значение y_i.

c)

Значения y_{i_max},, y_{i_min} можно взять из множества значений y_{i_,} для разных альтернатив

3) Мультипликативный способ свертки.

Критерий формируется в виде взвешенного произведения:

,

где P_i — весовые коэффициенты; P_i > 0 — для хороших частных критериев; P_i < 0 — для плохих частных критериев.

Часто для упрощения расчётов значения Pi принимаются равными ±1 и мультипликативный критерий приобретает вид:

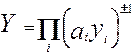, где a_i — весовые коэффициенты, a_i>0.

Пример: Основными частными критериями качества электронных микросхем служат быстродействие, помехозащищённость («хорошие» критерии) и потребляемая мощность («плохой критерий). Поэтому для интегральной оценки качества электронных микросхем часто используется следующий обобщенный мультипликативный критерий:

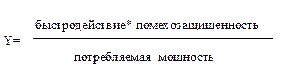
Мультипликативный критерий имеет такие же достоинства и недостатки, что и аддитивный. Мультипликативный критерий вытекает из принципа справедливой относительной компенсации. Он состоит в следующем. Будем считать для простоты, что все частные критерии «хорошие». Допустим, что, изменяя какие-то величины альтернатив, мы добиваемся увеличения некоторых частных критериев. Обычно из-за проблемы конфликтности ЗПР увеличение одних «хороших» частных критериев приводит к уменьшению других тоже «хороших» частных критериев. Возникает задача поиска компромисса между увеличением одних и уменьшением других критериев. В ЗПР справедливым считается такой компромисс, когда суммарный уровень относительного увеличения одних частных критериев равен суммарному уровню относительного увеличения значения других критериев

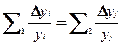
Здесь слева от равенства записана сумма относительных приростов одних хороших критериев, а справа – сумма относительного уменьшения других хороших критериев. Тогда можем переписать это равенство в виде:

 

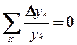
Если 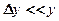, то справедливы следующие преобразования:

 

.

 

Так как логарифмическая функция монотонно возрастает с ростом аргумента, то её дифференциал может быть равен нулю только в том случае, если аргумент приобретает экстремальное значение (минимум или максимум), после чего начинает изменяться в обратную сторону. Отсюда если 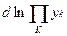=0, то (минимум, или максимум). Обозначение y_k играет роль 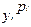или a_iy_i. По смыслу задачи аргумент положителен и может иметь только максимум. Таким образом, максимум мультипликативного критерия соответствует точке, где выполняется приведенное выше условие компромисса (равенство нулю суммы общих изменений частных критериев).