Типы шкалы для измерения критериев

Типы критериев в задачах принятия решений.

Основные требования к задачам принятия решения.

Глава 1. Описание задач принятия решения на содержательном уровне

Москва, 2009 год

Теория принятия инженерных решений

Конспект лекций по курсу

Валерий Николаевич Ильин

Підстави виникнення трудових правовідносин

 

 

 

 

 

 

1.1. Примеры задач принятия решения

Жизнь каждого человека — это цепь решений. Эти решения принимаются либо на бытовом уровне (куда пойти учится, как провести время), либо на инженерном уровне (выбрать тип компьютера, тип языка программирования, серию микросхем, вариант проекта) и т. д. Принятие решений на бытовом уровне специальных знаний не требует, так как оно основано на жизненном опыте и здравом смысле. Принятие решений на профессиональном уровне требует специальных знаний – теории принятия решений. Например, эта теория позволяет правильно ответить на вопрос, какой компьютер из двух предпочтительней: имеющий более высокое быстродействие, но меньший объём оперативной памяти, или наоборот? Или продажа какого вида товара из нескольких имеющихся на складе принесёт большую прибыль, если будущая конъюнктура (спрос на товар) заранее неизвестна – высокая или низкая? В данном курсе изучаются методы принятия решений на профессиональном уровне.

Не всякая задача может рассматриваться как задача принятия решений. Задача принятия решения – это задача выбора из нескольких имеющихся вариантов объекта, структуры или стратегии действий лучшего. Чтобы задача была задачей принятия решений, она должна удовлетворять двум основным требованиям.

1. В задаче должно быть не менее двух конфликтующих вариантов решения. Понятие конфликтности вариантов означает, что среди них нет явно предпочтительного. Например, при выборе лучшего компьютера из нескольких по критериям быстродействия и памяти не должно быть явно лучшего, имеющего наивысшее быстродействие и одновременно наибольший объём оперативной памяти, так как в этом случае выбор очевиден и знания теории не требует.

2. Необходимо иметь критерий, способ, правило для сравнения различных вариантов решения и выбора лучшего из них.

Критерии, используемые в задачах принятия решений, классифицируются следующим образом:

1. Количественные, выражаемые числом, например объём памяти компьютера, и качественные, не поддающиеся числовому выражению, например дизайн, внешний вид компьютера.

2. Объективные, значения которых не зависят от того, кто принимает решение, и субъективные, с значением, зависящим от мнения принимающего решение.

Пример:

Даны следующие характеристики микросхемы:

y₁ — потребляемая мощность;

y₂ — быстродействие;

y₃ — помехозащищенность.

Каждый из этих критериев – объективный. Объединим эти критерии в виде взвешенной суммы:

Этот критерий – субъективный, так как его численное значение зависит от субъективно задаваемых значений весовых коэффициентов a_i, определяющих важность каждого из объективных критериев для того, кто принимет решение о выборе лучшей микросхемы..

 

3. Частные, характеризующие только одно свойство или параметр имеющегося объекта, и обобщённые, характеризующие совокупность нескольких свойств или параметров. Например, в предыдущем примере потребляемая мощность, быстродействие, помехозащищенность – частные критерии, а их взвешенная сумма Y – обобщённый. Обобщённые критерии могут быть сильными и слабыми, о чём подробнее сказано ниже и далее в разделе 3.2.1.

 

4. Сильные, позволяющие найти среди множества альтернатив одну лучшую, и слабые, позволяющие найти среди множества альтернатив подмножество, в котором каждая альтернатива в определённом смысле не хуже и не лучше остальных в этом подмножестве, то есть все альтернативы в заданном смысле равноценны.

5. «Хорошие» критерии (чем они больше, тем лучше, например, память и быстродействие компьютера), и «плохие» с обратной зависимостью, например, потребляемая прибором мощность.

6. Скалярные, выражаемые одним числом, и векторные, представляющие собой вектор – совокупность нескольких чисел. Например, обобщённый критерий или один частный критерий – скаляры, а совокупность частных критериев – вектор.

7. Детерминированные, не учитывающие статистические свойства критериев, и статистические, учитывающие разброс параметров.

В рамках приведенной классификации потребляемая мощность, быстродействие – это детерминированные, частные, числовые, скалярные, объективные критерии.

Шкала — это способ оценки критерия. Наиболее распространенными являются следующие пять типов шкал:

1 Шкала наименований — перечислительная шкала. Она ставит в соответствие имени объекта число на шкале. Обычно таким числом является порядковый номер объекта. Это простейшая качественная шкала, так как на ней нельзя определить, что больше и что меньше, что лучше и что хуже, но можно найти объект по его номеру. Свойства объекта не зависят от его места на шкале наименований. Заметим, что перечисление фамилий в алфавитном порядке уже даёт информацию о месте объекта на шкале, зависящем от начальной буквы фамилии (чем «старше» эта буква в алфавите, тем дальше фамилия от начала шкалы) Такая шкала уже не является шкалой наименований и становится ранговой (см. далее).

Пример:

Очевидно, фамилиям можно присваивать номера в произвольном порядке.

 

2. Ранговая шкала — качественная шкала. Ранг объекта – это его порядковый номер объекта в последовательности предпочтений между объектами. Если объект Sа лучше объекта Sb, например выше ростом, то на ранговой шкале номер объекта Sа, то есть его ранг, больше номера (ранга) объекта Sb.

Пример: пусть имеем четыре объекта (человека) разного роста. Ранговая шкала роста имеет вид:

 

 

Автоматная шкала — перечислительная шкала автоматного времени. Её можно рассматривать как частный случай ранговой шкалы, в которой роль рангов играют номера моментов времени, в которые в цифровом автомате (устройстве с памятью) происходят какие-то события, например, переключения. Она ставит в соответствие каждому событию, входящему в последовательность событий, порядковый номер момента его появления. Эта шкала определяет последовательность возникновения событий, но не физическое время между ними. Длительность интервалов времени между моментами появления следующих друг за другом событий не играет роли. Считается, что все события разделены одинаковыми интервалами. По существу, автоматная шкала – это последовательность порядковых номеров последовательно возникающих событий.

Пример

4. .Шкала отношений— количественная шкала. Шкалы отношений — наиболее распространенные шкалы. В этих шкалах нуль отсчёта соответствует нулю измеряемой величины. Большинство количественных шкал, которыми мы пользуемся, – это шкалы отношений. Одну и ту же физическую величину можно измерять с помощью разных шкал отношений. Например, температуру можно измерять по шкале Цельсия (точка замерзания воды 0⁰С, а точка кипения 100⁰С) или по шкале Реомюра (точка замерзания воды 0⁰R, а точка кипения 80⁰R). Как видно из рисунка, обе шкалы проходят через общий нуль отсчёта, за который принята температура замерзания воды, но масштаб единиц измерения температур (градусов) у этих шкал разный. Очевидно, градус по Реомюру более весомый, чем по Цельсию. Чтобы найти соотношение ∆1⁰С/∆1⁰R между этими градусами, воспользуемся соответствием диапазонов температур между точками кипения и замерзания воды для каждой шкалы 100⁰С – 0⁰С = 80⁰R –0⁰R, откуда следует, что ∆1⁰С/∆1⁰R = 80/100 = 0,8 , то есть изменение температуры на один градус Цельсия соответствует изменению температуры на 0,8 градуса Реомюра. Таким образом, температуры этих двух шкал с разным масштабом единиц измерения связаны соотношением t⁰ R.= 0,8*t⁰ C. Например, 60⁰С соответствуют 0,8 х 60 = 48⁰ R. В общем случае измерения U и φ(U) в разных шкалах отношений связаны соотношением j(U) = K * U, где К – коэффициент пересчёта масштабов единиц измерения. В нашем случае при пересчёте температуры по Цельсию в температуру по Реомюру К=0,8, при обратном пересчёте К=1/0,8 = 1, 25.

5. Интервальная шкала. Иногда температуру указывают не в градусах по шкале Цельсия, а в градусах по шкале Фаренгейта. Например, в романе Жюль Верна о капитане Немо глава, в которой описывается «охота» фрегата за «Наутилусом», называется «48 градусов по Фаренгейту» – это температура воздуха во время охоты. А сколько это градусов по Цельсию?

Пример:

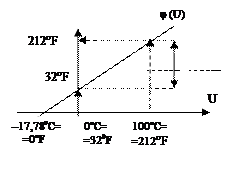Чтобы ответить на этот вопрос, сравним температурную шкалу по Фаренгейту и по Цельсию (см. рисунок). Шкала Фаренгейта относится к классу интервальных шкал, общим признаком которых является сдвиг относительно общепринятого начала координат. На шкале Фаренгейта за начало отсчёта, то есть за 0⁰F, принята температура таяния смеси снега с нашатырём, сдвинутая относительно нуля шкалы Цельсия (точки замерзания воды) на +­32⁰F. Таким образом, температура замерзания воды по Фаренгейту оказывается равной +­32⁰F, что соответствует 0⁰С. Кроме того, температура кипения воды, равная 100⁰С по шкале Цельсия, по Фаренгейту равна 212⁰F. Таким образом, разность ∆ между точками замерзания и кипения воды по шкале Цельсия составляет 100­⁰ C, а по шкале Фаренгейта 212⁰F – 32⁰F = 180⁰F. Следовательно, ∆180⁰F=∆100­⁰C, откуда ∆1⁰С=180/100=∆1,8⁰F, то есть. изменение температуры на один градус по Цельсию соответствует изменению температуры на 1,8 градуса по Фаренгейту. Кроме того, нужно учесть, что температура по Фаренгейту из-за сдвига начала отсчёта на 32⁰F ниже (меньше), чем по Цельсию. Таким образом, пересчёт известной нам температуры по Фаренгейту t⁰F в температуру t⁰C по Цельсию выполняется по формуле

t⁰С = (t⁰ F – 32*t⁰F)./1,8.

Правильность этой формулы подтверждается тем, что в соответствии с ней температура кипения воды по Фаренгейту 212⁰F по шкале Цельсия будет равна (212 – 32)/1,8 =100⁰С, а температура замерзания воды 32⁰F по шкале Цельсия будет равна (32 – 32) /.1,8 = 0⁰С. В соответствии с этой формулой 0⁰F соответствует ­–17,78⁰С, а упомянутые выше 48⁰F будут равны по шкале Цельсия всего лишь (48 – 32)./1,8 = 8,8⁰С. Пересчёт температуры по Цельсию в температуру по Фаренгейту производится по обратной формуле

t⁰F = 1,8*t⁰С + 32

в соответствии с которой 100⁰С равны 212⁰F, а 0⁰С равен 32⁰F.

В общем случае пересчёт величины U, измеренной в общепринятой шкале, проходящей через нуль, в величину j(U), измеренную в интервальной шкале, сдвинутой относительно нуля, производится с помощью линейной функции

j(U) = K1 + K2 * U,

где K₁ - сдвиг начала отсчета в интервальной шкале по отношению к обычной шкале; K₂ - коэфффициент, показывающий соотношение между единицами измерения в обычной и интервальной шкалах.

Интервальные шкалы — количественные, поэтому в них можно определить, насколько одна величина больше другой. Поскольку интервальные шкалы линейные, отношение отрезков (интервалов), измеренных в шкалах U и j(U), сохраняется постоянным: ∆U1/∆U2= j(∆U₁) / j₂(∆U₂) (отсюда название интервальных шкал). Но так как начало отсчета в интервальных шкалах сдвинуто относительно начала координат на величину К1, то отношение самих величин не постоянно: U1/U2 ≠ j(U₁) / j₂(U₂) = (К1+К2*U₁) / (К1+К2*U₂) Поэтому отношение двух температур, измеренных по шкале Фаренгейта, не будет равно отношению этих же температур, измеренных по шкале Цельсия. Например, если по Цельсию t1= 20⁰С , t2= 10⁰ С и t1/t2 = 2, то по Фаренгейту соответственно t1=68⁰F , t2= 50⁰ F и t1/t2 < 2. Но отношение интервалов, отмеренных на шкале Цельсия и на шкале Фаренгейта, сохраняется: (20 –0) / (10–0)= (68 –32) / (50–32)=2. Заметим, что шкалы отношений являются частным случаем интервальных шкал при К1=0. Поскольку в шкалах отношений нуль отсчёта совпадает с началом координат, в них сохраняется постоянным не только отношение интервалов, но и отношение самих величин.

Шкалы наименований, автоматная и ранговая называются перечислительными или порядковыми, а шкалы интервальная и отношений — численными.