Использование оценок для экспериментального определения вероятностных характеристик измерительных сигналов

 

Результат определения значения вероятностной характеристики по ограниченной совокупности выборочных данных (мгновенных значений реализации ) носит название оценки где - оператор, представляющий собой преобразования, лежащие в основе определения вероятностной характеристики массива выборочных данных .

К основным свойствам оценок относятся несмещенность , состоятельность и эффективность. Оценка называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемой характеристики при любом ее значении

Оценка называется состоятельной, если при бесконечном увеличении объема выборочных данных она сходится по вероятности к истинному значению оцениваемой характеристики

где n – объем выборки.

Эффективными называются оценки, дисперсия которых минимальна (могут быть найдены методом минимальных квадратов, методом максимального правдоподобия и т.д.).

В таблице 1 представлены виды оценок вероятностных характеристик, используемых при различных способах представления случайного процесса (ансамблем реализаций или последовательностей). Использование оценок, представленных в таблице, позволяет переходить от истинных значений, получаемых на основе использования моделей случайных процессов, к экспериментальным результатам измерений.

В таблице 1 использованы так называемые идеальные операторы усреднения:

- идеальный интегратор с нормированием по Т:

- идеальный сумматор с нормированием по n: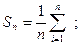

- идеальный интегратор – сумматор с нормированием по n и T: .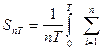

Приведенные в таблице 1 выражения оценок определяют разные виды характеристик. При усреднении по времени и по реализациям значение оценки не зависит ни от текущего времени, ни от номера реализации. Такая характеристика называется средней и обозначается θ­_ср­ .

При усреднении только по значениям реализаций выборочные значения соответствуют мгновенным значениям реализаций, взятым в один и тот же момент , вероятностная характеристика будет зависеть от текущего времени, она называется t – текущей вероятностной характеристикой θ­_t­. При усреднении только по времени, когда все выборочные значения относятся к одной и той же реализации, вероятностная характеристика будет зависеть от номера реализации, она называется k- текущей и обозначается θ­_k.

Выражения для приведенных выше видов оценок, приведены в таблице 2.

 

 

Таблица 1.

Расчетные формулы для нахождения статистических оценок случайных сигналов

Суть оценки	Представление случайного процесса ансамблем реализаций	Представление случайного процесса последовательностями
Усреднение значений по реализациям
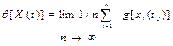
Усреднение значений во времени
Мгновенная оценка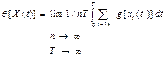

 

 

Таблица 2.

Виды статистических оценок измерительных сигналов