Z- преобразование и разностные уравнения

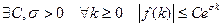ОпрПоследовательность комплексных чисел , обладающая свойством , называется оригиналом.

Опр Изображением (Z-преобразованием)оригинала называется функция

ЗАМЕЧАНИЕ Изображение является аналитической функцией с центром в бесконечно удаленной точке .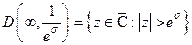

Обозначение 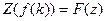или .

Пр 1 Единичный импульс (дельта-импульс Кронекера) 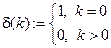имеет Z -преобразование .

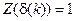Пр 2 Пусть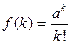. Тогда .

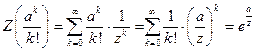Пр 3 Найдем оригинал по изображению .

.

ТЕОРЕМА 10.11(свойства Z- преобразования)

1)Множество оригиналов и множество аналитических в точке функций

являются векторными пространствами, а Z-преобразование является их изоморфизмом.

2)(связь с преобразованием Лапласа) Если по оригиналу 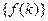построить ступенчатую функцию 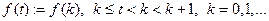, то изображение последней по Лапласу и Z-преобразование связаны равенством .

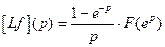3)(теорема опережения (смещения)).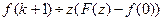

4)(дифференцирование изображений)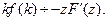

5)(свертка оригиналов)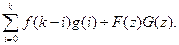

6) (сложная свертка) .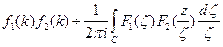

7)(формула обращения),где - спрямляемый жорданов контур, охватывающий бесконечно удаленную точку;

, если есть рациональная функция с полюсами.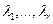

8) (масштабирование частоты) .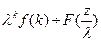

Пр Найдем оригинал по изображению 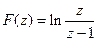, где .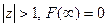

.

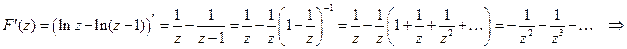
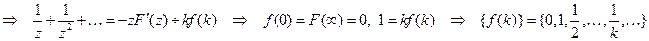ОпрСистема уравнений 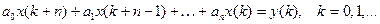(1)

где 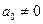, , 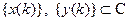называется линейным разностным уравнением n-го порядка с постоянными коэффициентами.

Опр Пусть даны числа . Решением разностного уравнения (1) с начальными данными 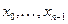называется последовательность чисел 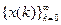которая удовлетворяет всем уравнениям (1) и начальным условиям .

ОпрРазностное уравнение (1) называется асимптотически устойчивым, если при любых начальных условиях соответствующее решение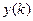однородного уравнения стремится к нулю: .

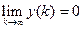ТЕОРЕМА 10.12(свойства решений разностного уравнения)

1) Для любой -ки чисел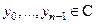решение задачи Коши для однородного разностно го уравнения с начальными условиями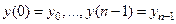существует и единственно

2) Пусть 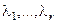есть нули кратностей соответственно 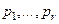характеристического многочлена 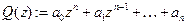. Тогда общее решение однородного уравнения имеет вид .

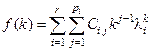Рассмотрим разностное уравнение вида

, (2)

с начальными условиями , где 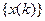- известный оригинал, а 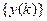- искомое решение. Обозначим ,

,

.

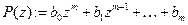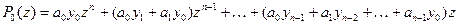Тогда:

3) решение однородного уравнения с заданными начальными условиями единственно и равно ;

4) решение неоднородного уравнения с нулевыми начальными условиями равно 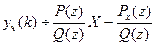, а его решение с исходными начальными условиями равно

;

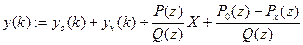5) Разностное уравнение(1)асимптотически устойчиво тогда и только тогда, когда нули его характеристического многочлена 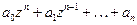по модулю меньше 1.

Пр 1 Решим разностное уравнение третьего порядка

где .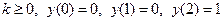

Так как 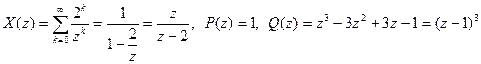, , 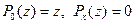то по последней теореме 10.12.4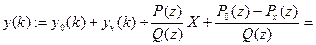

.

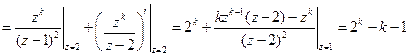Это есть искомое решение разностного уравнения с заданными начальными условиями.

Пр 2 Разностное уравнение является асимптотически устойчивым, так как корни его характеристического уравнения 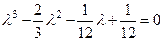лежат в единичном круге.

_____

ОпрПусть функции 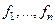определены на . Нормальной системой разностных уравнений (НСРУ) называется система вида 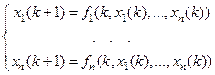. Или в матрич ном виде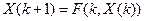. Нормальной системой линейных разностных уравнений (НСЛРУ) называется система вида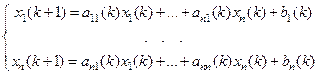

Или в матричном виде 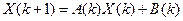. Если матрица 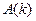не зависит от ,

последняя называется системой с постоянными коэффициентами.