Преобразование Лапласа

Опр Комплекснозначная функция на называется оригиналом, если она удовлетворяет условиям: 1) ; 2) ;

3) имеет не более конечного числа точек разрыва первого рода на .

ОпрЧисло называется показателем роста оригинала .

Кпр Функция не является оригиналом, так как имеет разрыв второго рода в точке . Функция не является оригиналом, так как .

Опр Изображением оригинала называется функция комплексного переменного

.

Обозначение - "функция является изображением оригинала ".

ОпрОтображение называется преобразованием Лапласа.

ЗАМЕЧАНИЕИзображение является аналитической функцией в полуплоскости .

Пр 1 Найдем преобразование Лапласа функции Хевисайда .

.

Пр 2 для .

ОпрНесобственный интеграл , называется гамма – функцией.

ЗАМЕЧАНИЕМожно доказать, чтогамма - функция является аналитической

функцией в области , а в точках она имеет простые полюсы.

Пр 1

.

Пр 2 .

Опр Сверткой оригиналов называется интеграл .

ТЕОРЕМА 10.9(свойства преобразований Лапласа).

1) Пусть – пространство оригиналов, пространство функций, аналитических в какой-либо правой полуплоскости. Тогда преобразование Лапласа является линейным.

2) (теорема подобия).

3) (теорема запаздывания).

4) (теорема смещения).

5) (изображение производной оригинала).

6) (оригинал производной изображения).

7) (изображение интеграла оригинала) .

8) (оригинал интеграла изображения).

9) (изображение свертки) .

10) (интеграл Дюамеля) .

11) (изображение произведения).

12) .

ЗАМЕЧАНИЕПусть функция имеет конечное число точек разрыва первого рода на отрезке и . Обозначим её изображение Образуем периодическую на функцию ,

и найдем изображение последней при , используя теорему запаздывания.

.

Пр Найдем изображение периодического импульсного сигнала ширины . Так как

,

то .

Отсюда, полагая , с помощью замечания находим изображение импульсного сигнала

.

ТЕОРЕМА 10.10(о восстановлении оригинала по изображению)

1) Пусть функция голоморфна в полуплоскости , и интегралабсолютно сходится. Тогда является изображением функции .

2) Пусть аналитическая в точке функция имеет ряд Лорана . Тогда её оригинал вычисляется по формуле .

3) Рациональная функция относительной степени с полюсами является изображением функции .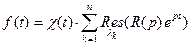

Приведем таблицу преобразований Лапласа некоторых элементарных функций.

 

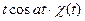
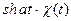
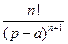
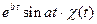
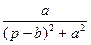
ЗАМЕЧАНИЕТеоремы 10.9, 10.10 и таблица преобразований дают метод решения ЛДУ -ого порядка, НСЛДУ, ЛДУЧП и интегральных уравнений.

Пр 1 Решим задачу Коши для НСЛДУс начальными условиями

Положим . По теореме об изображении производной .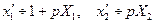

Применим преобразование Лапласа к каждому уравнению системы, используя свойство его линейности и таблицу.

.

Пр 2 Найдем решение интегрального уравнения .

Применяя преобразование Лапласа к левой и правой частям и используя теорему 10.9.9 и таблицу, получаем .

Правая часть имеет два простых полюса и полюс второго порядка. Тогда по теоремам 10.10.3 о восстановлении оригинала и 10.4 о вычислении вычетов в полюсах получаем

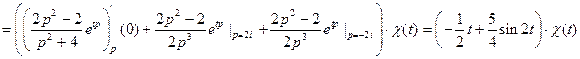ЗАМЕЧАНИЕВ Matlab прямое и обратное преобразования Лапласа производятся с помощью функций . Перед их исполнением все переменные и константы необходимо объявить символьными (функция ).