Описание процесса теплообмена для двигателя с открытой камерой сгорания

Рассмотрим процесс теплообмена в открытой КС. Примем следующие допущения: заряд в КС квазиравновесный, его движение – квазистационарное. Воспользуемся системой уравнений (18)-(21) из § 2.2 для ламинарного пограничного слоя.

Движение заряда на границе пограничного слоя будем считать градиентным (dP/dx не равен нулю). Будем также считать, что градиент давления одинаков как для ядра потока вблизи стенки, так и для самого пограничного слоя. Постановку задачи примем двумерную (рис. ХХ).

Рис. ХХ. К постановке задачи о конвективном теплообмене в КС ДВС
при градиентном течении газа вблизи стенки

На первом этапе решения задачи локального теплообмена находится распределение скоростей в пограничном слое. Рассмотрим некоторые положения данного решения.

Воспользуемся уравнением движения в ЛПС:

(131)

и уравнением сплошности:

(132)

Причем градиент давления вблизи стенки и распределение продоль-ной (касательной) скорости известно из (21):

Граничные условия для системы (131)-(132):

на стенках камеры сгорания: z = 0,

, в ядре потока:

(133)

При градиентном течении обычно используют аппроксимацию изменения скорости внешнего потока в виде:

(134)

где C – постоянная, m – параметр градиентности потока.

Введем функцию тока Y так, что:

(135)

При подстановке производных Y в уравнение сплошности (132) получаем его тождественное выполнение. Это позволяет избавиться от последнего, однако порядок произодных в уравнении движения при подстановке тех же производных увеличится.

Введем безразмерную функцию тока:

(136)

и безразмерную поперечную координату:

(137)

где d – текущая толщина динамического пограничного слоя.

Для ламинарного пограничного слоя в градиентных условиях:

(138)

В последних двух выражениях A(m) – функция параметра градиентности потока (рис. ХХ). При малых m толщина ЛПС максимальна, а с его ростом быстро падает. При m = –0,0904 пограничный слой теряет устойчивость.

Рис. ХХ. График изменения функции A(m)

Выразим размерную координату z из (137): z = c₁h, где c₁ – константа.

Тогда, поскольку , а , то

(139)

Или,

(140)

Таким образом, f ¢(h) – относительная скорость в пограничном слое с точностью до коэффициента c₁.

Далее в уравнении (131) осуществляется переход к безразмерной поперечной координате h и безразмерной функции тока f(h). В результате решения полученого уравнения находят f(h) и ее производную – безразмерное распределение скорости в пограничном слое f ¢(h). Далее будем считать, что они уже известны, а скоростная задача для ЛПС решена.

Далее переходят к задаче нахождения распределения температур в пограничном слое, для чего используют уравнение Фурье-Кирхгоффа:

(141)

с граничными условиями

при z = 0: T = T_w; при

: T = T_f.

(142)

Введем новую переменную J – приращение температуры относительно T_f: . После замены в (141) T на J получим:

(143)

где .

Граничные условия для (143):

при z = 0:

; при

(144)

где – известный температурный напор.

Подставим в выражение для безразмерной поперечной координаты (137) формулу (138) с учетом того, что :

(145)

Воспользуемся последним выражением для h и функциями f(h) и
f ¢(h) для модификации выражения (143). Условимся, что решение (143) будем искать в виде J = J(x,h), где h = h(x,z). Для этого выразим частные производные J(x,z), входящие в это уравнение, через производные более низших порядков.

Выразим :

(146)

Берем производную от h(x,z) из (145):

(147)

После подстановки (147) в (146) получим:

(148)

Выразим следующую производную:

(149)

Взяв производную от h по z (145), получим:

(150)

тогда

(151)

Далее определим вторую производную J по z с учетом (151):

(152)

Подставляя в (143) полученные производные, а также безразмерную функцию тока f и ее производную f ¢, уравнение энергии приводят к виду:

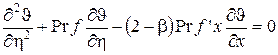(153)

где – характеристика степени градиентности потока.

Решение (153) с граничными условиями (144) с условием замены z на h (z = c₁h) ищем в виде:

(154)

Подставляя последнее выражение в (153) получим:

;

Разнеся переменные в разные части уравнения, получим:

(155)

где n – собственные числа решения.

После разделения переменных имеем систему уравнений:

(156) (157)

Решим (157), умножив его на следующее выражение:

После приведений в последнем:

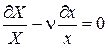(158)

Уравнение (158) можно проинтегрировать:

;

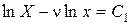потенцируя последнее выражение, получаем:

(159)

Подставляя полученное выражение в общее решение (154), имеем:

(160)

Дальше будем искать граничные условия 3-го рода, когда распределение температур в пограничном слое не зависит от распределения температур в стенке а, следовательно, и от продольной координаты x (T_w= const). Это возможно только в случае равенства нулю собственных чисел решения n, тогда:

(161)

где – полный температурный напор.

Далее, положив в (156) собственные числа решения равными нулю, решаем его со следующими граничными условиями:

(162)

Итак: , и

После интегрирования имеем:

В результате потенцирования получаем:

(163)

Интегрируем это выражение во второй раз, считая, что :

(164)

Согласуем решение (164) с граничными условиями (162):

на стенке, при ;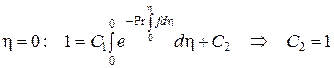

в потоке, при .

Подставив постоянные интегрирования в (164) получаем:

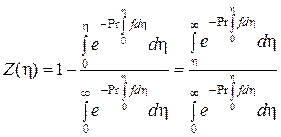(165)

Таким образом, распределение температур в пограничном слое найдено (в приращении от T_f по безразмерной поперечной координате h).

Перейдем теперь к определению граничных условий теплообмена (в виде ГУ 3-го рода):

(166)

Производную уже нашли, см. (151), следовательно:

(167)

Поскольку , то

(168)

Далее определим значение Z '(h) на стенке. Согласно (163):

(169)

Введем обозначение:

(170)

Подставляя (170) в (168) получим следующее:

Внеся x в подкоренное выражение, и выполнив переносы, имеем:

получаем окончательное выражение для интенсивности теплоотдачи:

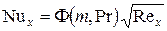(171)

Уравнение (171) представляет собой точное решение уравнения энергии в предположении ламинарности пограничного слоя и градиентном течении во внешнем потоке для граничных условий 3-го рода.

Функция Ф(m,Pr) – рассчитана и табулирована Г.Л. Эвансом и приводится в литературе в виде таблиц и графиков (рис. ХХ).