Критерии подобия и критериальные уравнения в учении о теплопередаче в ДВС

 

Остановимся на кратком рассмотрении критериев механического и теплового подобия, которые наиболее часто используются в описании процессов теплоотдачи в двигателях.

Критерии механического подобия.

1. Критерий Струхаля

,

где: l – путь (характерный геометрический размер); U – скорость потока;
t – характерное время протекания процесса.

Безразмерный комплекс Sh – гидродинамическое число гомохронности Струхаля, характеризующее отношение темпа изменения поля скорости в потоке жидкости к темпу изменения условий в среде. Иначе говоря, число Струхаля можно определить как меру отношения сил инерции, обусловленных нестационарностью движения, к силам инерции, обусловленным переносом количества движения в потоке. Поэтому число Струхаля является критерием кинематической нестационарности процесса движения жидкости или газа: если Sh³0,3 , то локальные ускорения соизмеримы с конвективными, движение нестационарно. В стационарных условиях Sh=0. Обычно движение считают квазистационарным, если Sh£0,3.

2. Критерий Эйлера

,

где: DP – приращение давления; r – плотность.

Число Эйлера есть мера отношения сил давления к силам инерции в потоке.

3. Критерий Рейнольдса

,

где: n– коэффициент кинематической вязкости.

Число Рейнольдса – мера отношения конвективных сил инерции к силам молекулярного трения (вязкости) в потоке. Данный критерий определяет режим течения в потоке и является практически основным в конвективной теплоотдаче.

4. Критерий Грасгофа

,

где: g – ускорение силы тяжести; b = 1/T – коэффициент объемного расширения жидкости.

Критерий Грасгофа характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей (при локальном нагреве или охлаждении). Данный критерий является определяющим в процессах свободной конвекции жидкости или газа.

Критерии теплового подобия.

5. Критерий Нуссельта

,

где: a – коэффициент теплоотдачи; l – коэффициент теплопроводности жидкости или газа.

Критерий Нуссельта является по своей сути безразмерным коэффициентом теплоотдачи и характеризует процесс конвективной теплоотдачи на границе раздела жидкость-твердая стенка при граничных условиях третьего рода. В задачах конвективного теплообмена этот критерий является искомой величиной.

6. Критерий Пекле

,

где: a – коэффициент температуропроводности.

Число Пекле представляет собой отношение количества теплоты, которое передано стенке конвекцией к количеству теплоты переданному теплопроводностью, или другими словами – есть мера отношения конвективного переноса теплоты к молекулярному.

7. Критерий Прандтля

,

где: r – плотность жидкости; c_p – удельная теплоемкость среды при постоянном давлении.

Критерий Прандтля – мера подобия полей температур и скоростей, или мера отношения интенсивностей переноса количества движения и количества теплоты; его также можно рассматривать как безразмерную теплофизическую константу жидкости.

8. Критерий Фурье

,

где: t – характерное время процесса.

Число Фурье есть мера отношения молекулярного переноса теплоты к локальному, оно пропорционально отношению темпа изменения условий в среде к темпу перестройки температурного поля. Данный критерий характеризует нестационарность теплового процесса.

9. Критерий Эккерта

,

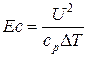где: DT – разность температур между газом и стенкой.

Критерий Эккерта представляет собой меру отношения теплоты, вызванной трением к молекулярному переносу теплоты в потоке. Данный критерий характеризует интенсивность диссипации энергии в потоке вследствие гидродинамического трения.

10. Критерий Больцмана.

,

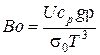где: s₀ – излучательная способность абсолютно черного тела; T – температура излучателя.

Число Больцмана есть мера отношения энтальпии потока к теплоте, переданной лучеиспусканием.

Критерии подобия могут быть определяющими и определяемыми.

Определяющие числа подобия могут быть полностью получены из исходных уравнений и условий однозначности. К ним относятся числа Re, Sh, Fo, Pe, Pr, Ec, Bo, Gr.

К определяемым критериям подобия относятся числа Nu и Eu, поскольку входящие в них величины не заданы условиями однозначности и являются искомыми.

При записи критериальных уравнений устанавливают связь между определяемыми и определяющими числами подобия. При рассмотрении процессов теплообмена газа со стенками нас интересует коэффициент теплоотдачи (к.т.о.), поэтому критериальное уравнение сложного нестационарного конвективного теплообмена (КТО), сопряженного с радиационной составляющей и диссипацией энергии в общем виде может быть представлено:

или, поскольку, , то:

(4)

Для решения отдельных частных случаев это уравнение можно упростить. Так, при стационарном (квазистационарном) движении и теплообмене выпадают критерии и 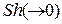. Если на процесс передачи теплоты не влияет диссипация энергии то . При вынужденном турбулентном движении можно пренебречь влиянием свободной конвекции (критерий ), тогда, для стационарного сложного конвективно-радиационного теплообмена:

(5)

и т.д. Однако обычно, учитывая различия в природе конвективного и радиационного теплообмена, последнее выражение разделяют на два:

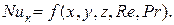(6)

(7)

Аналогичным образом теория подобия позволяет установить критериальные зависимости, справедливые для всех подобных процессов теплопередачи.