Обратная функция.

Рассмотрим функцию y=f(x), областью определения которой служит [a;b], а областью изменения [c;d]. Функция у ставит в соответствие каждой точке из [a;b] некоторую точку из [c;d]. Для изображенной функции можно установить и обратное соответствие: каждому значению y₀ из [c;d] соответствует единственное значение x₀ из [a;b], такое что y₀=f(x₀). Тем самым х можно рассматривать как функцию от y с областью определения [c;d], областью изменения [a;b]. Функцию x=g(y) назовем обратно по отношению к функции y=f(x).

Z.B Найти функцию, обратную к функции y=4.

Решение: 1) выразим из данной формулы х через у:

4; =;

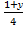2) Поменяем местами x и y: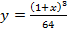

При каком условии существует функция, обратная к функции f(x)? Видимо, если из соотношения y=f(x) переменную х можно однозначно выразить через y.

Пример: 1) y=|x|. Выразить однозначно х через у нельзя. 2) у=х²; x=, x=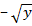. Тоже однозначно нельзя выразить.

Мы видим, что прямая у=у₀ пересекает графики функций более, чем в одной точке. Для у₀ мы не можем однозначно найти х. Итак, функция у=f(x) имеет обратную, если уравнение f(x₀)=y₀ при любом y₀ имеет не более одного решения. Это условие выполняется для строго монотонной функции.

Достаточный признак существования обратной функции:

Если функция строго возрастает (убывает) на множестве X, то для неё существует обратная.

Самостоятельная работа №1. Колмогоров Алгебра 10-11, стр 239 теорема.

Самостоятельная работа №2. Башмаков Алгебра 10-11 стр 213-214 Свойства взаимно обратных функций.