Введение
Содержание
Введение …………………………………………………………………………….. 5
1 Лекция 1. Введение. Динамика твердого тела ………………………………….. 6
1.1 1.1 Механическое движение. Пространство и время. Система отсчета…… 7
1.2 1.2 Основная задача механики. Уравнение движения твердого тела………. 7
1.3 1.3 Основные понятия динамики вращательного движения: момент импульса, момент силы, момент инерции…………………………………………… 8
2 2 Лекция 2. Энергия, работа, мощность………………………………………… 10
2.1 2.1 Энергия как общая мера различных форм движения материи…………10
2.2 2.2 Кинетическая энергия и работа силы…………………………………….11
2.3 2.3 Консервативные и неконсервативные силы. Потенциальное поле сил. 13
3 Лекция 3. Законы сохранения в механике………………………………………. 15
3.1 Закон сохранения импульса ………………………………………………15
3.2 Закон сохранения момента импульса …………………………………...15
3.3 Закон сохранения энергии в механике …………………………………….16
4 Лекция 4. Принцип относительности. Элементы релятивистской механики ….17
4.1 Принцип относительности Галилея ……………………………………. 17
4.2 Постулаты Эйнштейна. Специальная теория относительности ………... 19
4.3 Преобразования Лоренца …………………………………………………..20
4.4 Инварианты специальной теории относительности …………………….. 21
4.5 Элементы релятивистской динамики ……………………………………. 21
5 Лекция 5. Статистические распределения ………………………………………. 22
5.1 Статистический и термодинамический методы исследования ……….. 22
5.2 Закон равномерного распределения энергии по степеням свободы … . 23
5.3 Закон Максвелла для распределения молекул по скоростям …………. 24
5.4 Закон Больцмана для распределения частиц во внешнем потенциальном поле ………………………………………………………………………………….. 25
6 Лекция 6.Основы термодинамики ……………………………………………….. 26
6.1 Теплота и работа как формы обмена энергией в термодинамике. Первое начало термодинамики …………………………………………………………… 26
6.2 Второе начало термодинамики ……………………………………….. 27
7 Лекция 7. Явления переноса ……………………………………………………. 31
7.1 Общая характеристика явлений переноса ……………………………… 31
7.2 Элементы молекулярно-кинетической теории явлений переноса …… 33
8 Лекция 8. Электростатическое поле в вакууме …………………………………. 35
8.1 Электрический заряд …………………………………………………….. 35
8.2 Электростатическое поле. Характеристики электростатического поля 35
8.3 Основная задача электростатики …………………………………………38
8.4 Основные теоремы электростатики в вакууме …………………………. 38
9 Лекция 9. Электростатическое поле в веществе ………………………………… 39
9.1 Диэлектрики. Поляризация диэлектриков ……………………………… 39
9.2 Поляризованность. Объемные и поверхностные связанные заряды …. 40
9.3 Вектор электрического смещения. Теорема Гаусса для электростатического поля в диэлектрике ……………………………………………………….. 42
9.4 Условия на границе двух диэлектриков ………………………………. 43
10 Лекция 10. Энергия электрического поля …………………………………….. 44
10.1 Энергия взаимодействия системы зарядов ……………………………44
10.2 Энергия уединенного проводника и конденсатора …………………. 45
10.3 Энергия электрического поля …………………………………………. 45
11 Лекция 11. Постоянный электрический ток ………………………………….. 46
11.1 Общие характеристики и условия существования тока ………………46
11.2 Уравнение непрерывности. Условие стационарности электрического тока ………………………………………………………………………………….. 47
11.3 Классическая электронная теория электропроводности металлов … 48
12 Лекция 12. Магнитное поле в вакууме …………………………………………50
12.1 Магнитное поле. Вектор магнитной индукции ……………………… 50
12.2 Принцип суперпозиции. Закон Био-Савара-Лапласа …………………51
12.3 Магнитный поток. Основные законы магнитного поля …………….. 52
12.4 Работа перемещения проводника с током в магнитном поле ……… 53
12.5 Эффект Холла ………………………………………………………….. 53
13 Лекция 13. Магнитное поле в веществе ………………………………………. 54
13.1 Намагничивание вещества. Намагниченность ………………………. 54
13.2 Основные теоремы магнитостатики для поля в веществе …………. 55
13.3 Граничные условия для магнитного поля. Расчет магнитных полей в неоднородных средах………………..…………………………………………… 57
Конспект лекций «Физика 1» представляет собой очень краткое изложение содержания лекций по этой дисциплине для энергетических специальностей бакалавриата.
В каждой лекции отражены основные вопросы темы в их логической связи и структурной целостности, но без детальной проработки математических выкладок или примеров. Поэтому данная учебно–методическая разработка может и должна служить лишь ориентировочной основой для учебной деятельности студента, как на лекционном занятии, так и в самостоятельной работе вне аудитории.
Задание конкретных целей учения в каждой лекции, форма изложения учебного материала, адекватная, на наш взгляд, его содержанию, делает этот материал хорошо воспринимаемым, организованным внешне, что, в конечном счете, будет способствовать лучшему его усвоению, систематизации СРС по освоению курса «Физика 1».
Настоящий конспект лекций предназначен студентам электро– и теплоэнергетических специальностей. Программы «Физика 1» для этих специальностей имеют общее содержание, отличающееся лишь глубиной проработки некоторых разделов, что достигается всей системой учебно–методического обеспечения учебного процесса по каждой специальности, и в краткой учебно–методической разработке не может быть отражено.
1 Лекция 1. Введение. Динамика твердого тела
Цели лекции:
- осмыслить назначение курса физики и предмет физической науки;
- уяснить смысл основной задачи механики и сущность методов её решения.
Введение
Одного лоцмана спросили: «Как вам удается запомнить все подводные камни и мели?» Ответ был таков: «Мне нет дела до всех этих мелочей. Я плыву по фарватеру»
Физика в техническом вузе выполняет общеобразовательную функцию, дает будущему специалисту фундаментальные базовые знания, формирует его инженерно – техническое мышление и создает целостное представление о современной естественно – научной картине мира.
Современная физика изучает наиболее общие законы неживой природы и их частные проявления на любых структурных уровнях организации материи. Объект исследований физики – все многообразие неживой природы (поля, элементарные частицы, молекулы, макротела, космические среды, вакуум и т.д.). Мир изученных (и изучаемых) в настоящее время материальных явлений характеризуется очень широким диапазоном пространственных и временных областей (рисунок 1.1).
микромир макромир
10-18 10-12 10-6 1 106 1012 1026 r, м
Элементарные размер размер радиус размер видимой
частицы атома человека Земли части вселенной
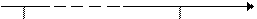t, с
10-23 1018 (десятки млрд. лет)
Рисунок 1.1 – Границы изучаемых явлений в физике
Принципиально важно то, что количественные изменения физических объектов и областей пространства, в которых происходят физические явления, сопровождаются качественными изменениями характера законов, их описывающих. Поэтому важно знать характерные значения соответствующих физических величин. Так естественным масштабом скоростей в природе является скорость распространения света в вакууме с = 3∙108 м/с. С ней связано качественное отличие нерелятивистских движений (v<<c) от релятивистских ( v~с). С постоянной Планка ħ = 1,054∙10-34 Дж·с связано разграничение законов физики на квантовые и классические.
Физика – наука экспериментальная и, одновременно, всесторонне теоретизированная. Она выработала эффективные методы «свертывания» информации (огромный фактический материал) благодаря четкой иерархии физических законов: от небольшого числа основных законов и фундаментальных принципов – к частным, имеющим конкретную практическую значимость в той или иной области профессиональной деятельности специалиста.
1.1 1.1 Механическое движение. Пространство и время. Система отсчета
Предметом механики является изучение механического движения тел и связанных с этим движением взаимодействий между телами. Под механическим движением понимают изменение взаимного положения тел или их частей в пространстве со временем.
Понятия пространства и времени есть тот фундамент, на котором строится физическая теория. Пространство и время не существуют отдельно от материи, это формы существования материи, органически связанные между собой. Пространство выражает порядок сосуществования материальных объектов, время – порядок смены явлений.
Абстрактные математические модели пространства и времени (например, эвклидово пространство) в большей или меньшей степени отражают свойства реальных пространства и времени, изучение которых является одной из основных задач вузовской физики.
Всякое движение относительно. Для описания механического движения необходимо выбрать систему отсчета: совокупность тела отсчета, системы координат и часов.
1.2 1.2 Основная задача механики. Уравнение движения твердого тела
Основной задачей механики является определение состояния изучаемой системы (материальная точка, совокупность материальных точек, твердое тело) в любой момент времени, если известно состояние этой системы в начальный момент.
В классической механике состояние частицы полностью характеризуется заданием в данный момент времени трех её (координат (x,y,z) и трех проекций (рx, рy, рz)импульса).
Твердое тело может совершать разнообразные сложные движения (примеры из техники). Все они, вообще говоря, могут рассматриваться как сложение двух простых: поступательного и вращательного. Поступательное движение твердого тела эквивалентно движению частицы с массой, равной массе тела, и помещенной в его центр инерции. При вращательном движении твердого тела вокруг закрепленной оси все точки тела движутся по окружностям, центры которых лежат на этой оси. В этом случае состояние тела может быть задано углом поворота вокруг оси и угловой скоростью.
1.3 1.3 Основные понятия динамики вращательного движения: момент импульса, момент силы, момент инерции
 |
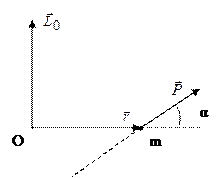Рисунок 1.2
Момент импульса частицы относительно точки О называется вектор, равный
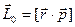, (1.1)
где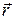 
– радиус вектор частицы в данный момент времени,
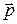– ее импульс (
).
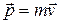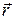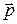Вектор момента импульса перпендикулярен плоскости, в которой лежат векторы и (рисунок 1.2).
Момент импульса системы частиц равен векторной сумме моментов импульсов всех частиц системы
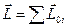(аналогично: 
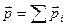). (1.2)
Моментом силы относительно точки О называется вектор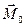 
равный
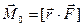, (1.3)
где 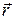– радиус–вектор точки приложения силы 
.
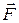Момент силы характеризует способность силы вызывать вращение тела вокруг точки, относительно которой он берется. Тело, закрепленное в точке О, под действием силы 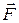повернется вокруг оси, совпадающей с направлением момента 
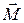(рисунок 1.3).
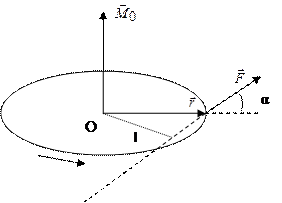
Рисунок 1.3
Взяв производную по времени от (1.1), можно показать, что скорость изменения момента импульса частицы определяется моментом силы
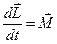. (1.4)
Соотношение (1.4) есть уравнение моментов.
Пусть твердое тело может вращаться вокруг закрепленной оси Oz. К телу приложена сила . Моментом силыотносительно оси Oz называется проекция Мz момента силы 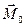относительно точки О. Он характеризует способность данной силы вызвать вращение вокруг данной оси и равен
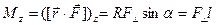, (1.5)
где l – плечо силы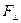 
, равное R sin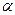
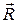– радиус-вектор, проведенный от оси в точку приложения силы в плоскости, перпендикулярной оси;
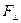– проекция силы 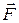на эту плоскость.
Чтобы определить момент импульса тела относительно оси, надо взять проекцию на эту ось суммарного момента импульса относительно точки О всех частиц этого тела (рисунок 1.4)
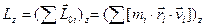. (1.6)
Легко убедиться в том, что это выражение (1.6) можно преобразовать к ввиду
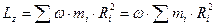. (1.7)
Величина
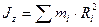. (1.8)
называется моментом инерции тела относительно оси. Момент инерции зависит от распределения массы тела вокруг оси и характеризует инертные свойства тела при вращательном движении. Таким образом, имеем
 |
Рисунок 1.4
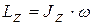, или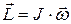 
. (1.9)
Из (1.4) и (1.5) с учётом (1.9) получим
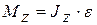, (1.10)
где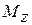 
– момент всех сил, приложенных к телу, относительно оси Z;
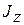– момент инерции тела относительно данной оси;
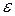– угловое ускорение вращающегося тела.
Выражение (1.10) представляет собой основной закон динамики вращательного движения твердого тела вокруг неподвижной оси.
2 Лекция 2. Энергия, работа, мощность
Цели лекции:
- усвоить понятия: энергия, работа, мощность;
- овладеть методом расчета различных видов энергии.
2.1 Энергия как общая мера различных форм движения материи
Существует много форм движения материи. Механическое движение – простейшая из них. Для его количественного описания мы использовали понятие импульса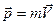 
. Количественной характеристикой теплового движения служит температура Т, электрического поля –
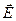и т.д. Все эти величины отражают качественные особенности различных форм движения материи. Но различные формы движения обнаруживают взаимную превращаемость. Следовательно, необходимо введение такой физической величины, которая относится ко всем формам движения материи и отражает их взаимную превращаемость. Такой физической величиной является энергия – одно из наиболее общих понятий в физике.
Энергия есть единая мера различных форм движения материи.
(Следует заметить: понятие энергии не «открыто», а именно введено в физику. Это продукт мыслительной деятельности человека.)
Так как движение есть неотъемлемое свойство материи, то всякая система обладает энергией. Энергия системы количественно характеризует эту систему с точки зрения возможных в ней изменений (количественных и качественных). Энергия - функция состояния.
В природе непрерывно идут процессы, в которых механическое движение и энергия передаются от одних тел к другим. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно охарактеризовать процесс обмена энергиями между взаимодействующими телами, в механике рассматривают работу силы, приложенной к данному телу. Работа есть мера изменения энергии в процессах силового взаимодействия.
2.2 Кинетическая энергия и работа силы
Рассмотрим некоторую частицу массы m. Подействуем на неё силой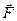 
. Уравнение второго закона Ньютона для этой частицы:
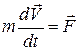. (2.1)
Умножим скалярно уравнение (2.1) на вектор бесконечно малого перемещения частицы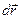 
(учтем, что = 
)
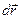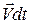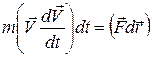. (2.2)
Из рисунка 2.1 видно, что скалярное произведение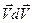 
равно
.
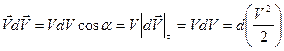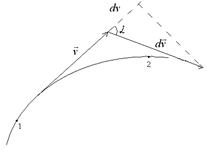
Рисунок 2.1
Следовательно,
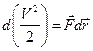. (2.3)
Величина в правой части уравнения (2.3) называется работой dA силы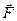
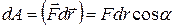, (2.4)
где α – угол между силой 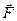и перемещением 
.
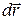Формула (2.4) выражает элементарную работу силы 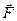. При перемещение тела на конечное расстояние полная работа выражается криволинейным интегралом вдоль траектории движения
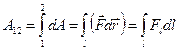. (2.5)
Работа силы – величина алгебраическая, она может быть положительной, отрицательной и равна нулю. Графическое представление работы показан на рисунке 2.2:
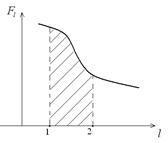
Рисунок 2.2
Рассмотрим левую часть уравнения (2.3). Она представляет собой полный дифференциал некоторой функции
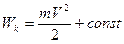. (2.6)
Величина Wk называется кинетической энергией частицы. Кинетическая энергия – это часть полной энергии частицы, связанная с её движением. Естественно предположить, что покоившееся тело (V=0) не обладает кинетической энергией, тогда из (2.6) следует что
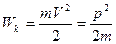. (2.7)
При вращательном движение твердого тела вокруг неподвижной оси его кинетическая энергия равна
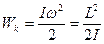. (2.8)
Выражения (2.7) и (2.8) справедливы только для нерелятивистских частиц (v<<c). Уравнение (2.7) справедливо и в случае, когда на частицу действует несколько сил. Тогда А12 – сумма работ всех сил. Таким образом, изменение кинетической энергии частицы равно работе всех сил, действующих на эту частицу.
А12=Wk2-Wk1 . (2.9)
Физическая величина, равная работе, отнесенной к единице времени, называется мощностью
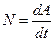. (2.10)
2.3 Консервативные и неконсервативные силы. Потенциальное поле сил
Все силы, независимо от их физической природы, принято делить на два класса: консервативные и неконсервативные. Сила называется консервативной, если её работа не зависит от того, по какой траектории перемещается частица из начальной точки в конечную.
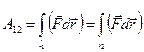. (2.11)
Если перемещение происходит по замкнутому пути, работа консервативной силы равна нулю
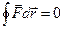. (2.12)
Консервативными являются центральные силы (гравитационные, кулоновские), сила тяжести, сила упругости.
Работа неконсервативной силы зависит от пути, по которому происходит перемещение. Примером таких сил являются сила трения, сила сопротивления среды. Работа силы трения всегда отрицательна. Такие силы называются диссипативными.
Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке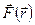 
. Силовые поля являются векторными. Силовое поле может быть однородным (поле силы тяжести), центральным (гравитационное поле). Поля консервативных сил обладают рядом характерных свойств, они образуют класс потенциальных полей. Такое поле в каждой точке можно охарактеризовать некоторой функцией Wp(
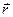), зависящей от положения точки в пространстве и характера силы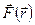таким образом, что работа консервативной силы 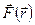при перемещении частицы между точками 1 и 2 будет равна убыли функции Wp
A12 =Wp1 –Wp2 =-∆Wp . (2.13)
Функция Wp называется потенциальной энергией частицы во внешнем консервативном поле. Из (2.13) следует, что работа в таком поле совершается за счет потенциальной энергии.
Потенциальная энергия частицы Wp(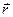) всегда имеет смысл энергии взаимодействия с объектами, создающими поле. Формула (2.13) позволяет в каждом конкретном случае получить выражения для Wp (с точностью до произвольной постоянной).
Получим связь между силой и энергией частицы, находящейся в потенциальном поле. Для этого запишем элементарную работу
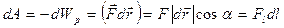. (2.14)
Проекция силы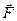на произвольное направление l:
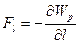. (2.15)
Взяв в качестве направления перемещения направления вдоль осей координат x, y, z, получим
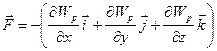, (2.16)
или
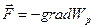. (2.17)
Формула (2.17) выражает связь между энергией и силой в потенциальном поле.
3 Лекция 3. Законы сохранения в механике
Цели лекции:
- - уяснить смысл законов сохранения как фундаментальных законов природы;
- - усвоить их формулировки и границы применения.
Законы сохранения импульса, момента импульса и энергии выделяются среди других законов своей всеобщностью. Это фундаментальные законы природы, которые выполняются не только в классической, но и в релятивистской физике и квантовой механике.
Все законы сохранения были открыты вначале опытным путем как обобщение огромного количества экспериментальных фактов. Позже пришло понимание глубокой взаимосвязи этих законов, позволившее не только осмыслить их всеобщность, но и предсказать в каких условиях тот или иной закон сохранения может видоизменять свою форму.
3.1 Закон сохранения импульса
Закон сохранения импульса есть общий закон природы, в основе которого лежит однородность пространства, т.е. одинаковость свойств пространства во всех ее точках.
Закон сохранения импульса соблюдается только для изолированных систем. Действительно, если система помещена во внешнее поле сил, то для нее разные области пространства уже не будут эквивалентны.
Изолированной, или замкнутой, системой называется система (совокупность взаимодействующих между собой тел), на которую не действуют внешние силы.
Полный импульс замкнутой системы материальных точек (тел) не изменяется с течением времени
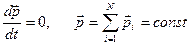. (3.1)
3.2 Закон сохранения момента импульса
При выводе основного закона динамики вращательного движения мы рассматривали твердое тело как систему материальных точек и пришли к соотношению
, (3.2)
где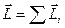 
– момент импульса системы;
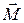– суммарный момент внешних сил, действующих на систему.
Сумма моментов внутренних сил всегда для любой системы равна нулю.
Если внешние силы отсутствуют (система замкнута), то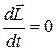 
, следовательно 
.
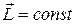Момент импульса замкнутой системы материальных точек (тел) остается постоянным
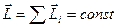. (3.3)
Если тело вращается вокруг неподвижной оси и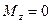 
, то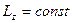 
. Учитывая , что 
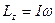, получаем
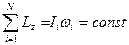. (3.4)
Закон сохранения момента импульса подобно закону сохранения импульса является фундаментальным законом природы. В основе его лежит свойство изотропности пространства, т.е. поворот замкнутой системы как целого не отражается на ее механических свойствах.
3.3 Закон сохранения энергии в механике
Закон сохранения и превращения энергии является одним из фундаментальных законов природы. В основе сохранения энергии лежит однородность времени, т.е. равнозначность всех моментов времени. Разные моменты времени эквивалентны в том смысле, что любой физический процесс протекает одинаковым образом независимо от того, когда он начался. Закон сохранения и превращения энергии имеет глубокий физический смысл. Он подтверждает положение о том, что движение является неотъемлемым свойством материи, оно несотворимо и неуничтожимо, а лишь преобразуется из одних форм в другие.
Рассмотрим полную механическую энергию частицы и системы частиц.
Вернемся к формуле (2.9). Пусть на частицу действуют консервативные силы 
и неконсервативные
. Тогда
Wk2–Wk1=A12*+A12 .
Так как A12*=Wp1–Wp2 , получим
(Wk2+Wp2)–(Wk1+Wp1)=A12 . .(3.5)
Полная механическая энергия частицы W есть сумма её кинетической и потенциальной энергий. Изменение полной механической энергии частицы, находящейся в поле консервативных сил, равно работе неконсервативных сил, действующих на частицу
W2–W1=A12 .(3.6)
Энергия системы N невзаимодействующих частиц определяется как сумма всех энергий частиц, составляющих данную систему
. (3.7)
Если частицы взаимодействуют между собой, следует учесть энергию их взаимодействия, которая уже не является аддитивной величиной
.(3.8)
Если между частицами системы действуют только консервативные силы (такая система называется консервативной), а внешние силы отсутствуют (A12 =0), то ее полная механическая энергия сохраняется, как это следует из формулы (3.6). Это утверждение и есть закон сохранения полной механической энергии. Очевидно, что полная механическая энергия сохраняется лишь для замкнутой консервативной системы тел.
Законы сохранения импульса, момента импульса и энергии стали весьма мощным и эффективным инструментом исследования. Эта важная роль законов сохранения обусловлена рядом причин:
- - законы сохранения не зависят ни от траекторий частиц, ни от характера действующих сил. Поэтому они позволяют получить ряд весьма общих и существенных заключений о свойствах различных механических процессов, не вникая их детальное рассмотрение с помощью уравнений движения;
- - этот факт позволяет использовать законы сохранения даже тогда, когда силы вообще неизвестны (столкновения тел, молекул).
4 Лекция 4. Принцип относительности. Элементы релятивистской механики
Цель лекции:
- уяснить сущность механического принципа относительности и основных принципов специальной теории относительности, а так же следствий из них.
4.1 Принцип относительности Галилея
Принцип относительности Галилея (механический принцип относительности) отражает фундаментальное свойство природы: никакими механическими опытами, проводимыми в инерциальной системе отсчета, нельзя установить, движется ли эта система отсчета прямолинейно и равномерно или покоится.
Принципу относительности Галилея соответствуют преобразования координат Галилея. Если оси двух инерциальных систем отсчета параллельны и относительное движение происходит вдоль одной из них (например, вдоль оси х) (рисунок 4.1), преобразования Галилея (прямые и обратные) имеют вид:
Рисунок 4.1
(4.1)
где 
– скорость системы К` относительно условно неподвижной системы К.
Физические величины, которые при преобразованиях Галилея остаются неизменными, называются инвариантами преобразований Галилея.
Одной из таких величин является ускорение
(4.2)
,
что обеспечивает и инвариантность всего второго закона Ньютона
Среди основных инвариантов классической механики отметим пространственный интервал 
(т .е. расстояние между двумя пространственными точками)
, (4.3)
а так же временной интервал
. (4.4)
К неинвариантным величинам в классической механике относится скорость. Классический закон сложения скоростей:
. (4.5)
Принцип относительности и преобразования Галилея отражают представления об абсолютном пространстве и абсолютном времени, которые лежат в основе классической механики.
4.2 Постулаты Эйнштейна. Специальная теория относительности
Специальная теория относительности (СТО) – это физическая теория пространства и времени, в которой предполагается, что пространство однородно и изотропно, время – однородно.
В основе специальной теории относительности Эйнштейна лежат два постулата: обобщенный принцип относительности и принцип постоянства скорости света в вакууме:
- все физические явления в инерциальных системах отсчета протекают одинаково.
- скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света, т.е. является универсальной постоянной. Она равна
м/с.
Следствия из основных постулатов Эйнштейна:
- время течет по-разному в разных инерциальных системах отсчета. Утверждение о том, что между двумя данными событиями прошел определенный промежуток времени, приобретает смысл только тогда, когда указано, к какой системе отсчета это утверждение относится; события, одновременные в некоторой системе отсчета, могут быть неодновременными в другой системе;
- относительность временных интервалов одного и того же события в системах отсчета К и К` :
. (4.6)
Время, отсчитываемое по часам, движущимся вместе с объектом, называется собственным временем этого объекта. Обозначим его 
, тогда
(4.7)
Движущиеся часы идут медленнее неподвижных. Замедление хода времени в системе, где часы покоятся, не является кажущимся и не связано с влиянием движения часов на их работу, а отражает относительный характер времени. Итак, не существует единого мирового времени. Время, его течение, понятия одновременности событий – относительны.
Относительность пространственных интервалов
(4.8)
Длина стержня 
, измеренная в системе отсчета, в которой стержень неподвижен, называется собственной. Как видно из (4.8), эта длина является максимальной, т.е. во всех системах отсчета длина тел уменьшается по сравнению с собственной. Это явление называется лоренцевым сокращением размеров тел в направлении движения. Лоренцево сокращение геометрических размеров тел не является кажущимся и не связано с физическим воздействием движения на размеры тела. Оно отражает неабсолютность пространственных интервалов, их зависимость от выбора системы отсчета.
4.3 Преобразования Лоренца
Релятивистские преобразования координат и времени, отражающие свойства пространства и времени в специальной теории относительности, называются преобразованиями Лоренца. Согласно этим преобразованиям переход от системы К` к системе К осуществляется по формулам (4.9), а от К к системе К` – по формулам (4.10)
. (4.9)
(4.10)
На основе полученных преобразований координат и времени можно дать еще одну формулировку принципа относительности: физические законы инвариантны относительно преобразований Лоренца.
Рассмотрим некоторые следствия из преобразований Лоренца. Во-первых, преобразования Лоренца наглядно демонстрируют неразрывную взаимосвязь пространственных и временных свойств нашего мира. Таким образом, нельзя говорить отдельно о пространстве и отдельно о времени, правильно будет говорить о пространстве – времени, в котором существует наш мир. Иными словами, наш мир четырехмерен.
Во-вторых, на основе преобразований Лоренца можно описать относительность одновременности, о которой мы ранее говорили на качественном уровне.
В-третьих, оказывается, что выражаемый формулой (4.5) классический закон сложения скоростей несправедлив при движении тел со скоростями, близкими скорости света. Релятивистский закон сложения скоростей для случая, когда частица движется вдоль оси Х
(4.11)
4.4 Инварианты специальной теории относительности
Из преобразований Лоренца следует, что скорость света одна и та же в различных инерциальных системах отсчета. Этот вывод соответствует принципу постоянства скорости света. Из формул преобразований Лоренца следует также, что скорость света является максимальной .
В релятивистской механике инвариантность пространственных и временных интервалов относительно преобразований Лоренца не имеет места. Возникает вопрос, нельзя ли в специальной теории относительности указать величину, связанную с пространственными и временными интервалами между двумя событиями, которая была бы инвариантна преобразованиям Лоренца? Этот вопрос решается положительно. Таким инвариантом в специальной теории относительности является величина 
, определяемая соотношением
. (4.12)
Эта величина называется пространственно – временным интервалом (или просто интервалом) между событиями.
4.5 Элементы релятивистской динамики
Релятивистский импульс выражается формулой
. (4.13)
С учетом выражения (4.13) основной закон динамики, представленный соотношением
Полная энергия включает и энергию движения, т.е. кинетическую энергию. Поэтому кинетическая энергия тела определяется как разность между полной энергией и энергией покоя Взятые раздельно друг от друга энергия W и импульс р относительны, то есть, различны в разных системах отсчета. Однако взятые совместно в виде комбинации 5 Лекция 5. Статистические распределения Цели лекции: - - уяснить сущность статистического и термодинамического методов исследования, предмет данной науки; - - изучить основные законы классической статистической физики. 5.1 Статистический и термодинамический методы исследования Статистическая физика и термодинамика – два взаимосвязанных раздела физики, изучающих наиболее общие свойства макроскопических физических систем, включая и такие системы, которые непосредственно связаны с нашим жизнеобеспечением. Задачей термодинамики является изучение свойств материальных тел, характеризуемых непосредственно измеряемыми в опытах величинами (макроскопическими параметрами: объемом, температурой, давлением и т.д.), на основе наиболее общих абсолютно верных принципов – начал термодинамики. При этом не привлекаются никакие модельные представления о строении вещества. Сила термодинамики в том, что её выводы верны в такой же степени, в какой верны начала термодинамики. Статистическая физика основана на модельных атомо-молекулярных представлениях о строении макротел (например, модель идеального газа) и математической статике. Свойства макросистем, в конечном счете, определяются свойствами частиц системы, особенностями их движения и усреднёнными значениями динамических характеристик этих частиц (энергии, скорости и т.д.). Статистическая физика дает способы вычисления подобных средних и с их помощью определяет макропараметры систем. Так было получено основное уравнение молекулярно-кинетической теории где p 
. (4.16)
они образуют абсолютную характеристику состояния частицы, инвариантную относительно преобразовании Лоренца. Из инвариантности этой величины вытекает релятивистская взаимосвязь между импульсом и энергией – при переходе из одной инерциальной системы в другую, импульс и энергия частицы изменяются так, что комбинация остается неизменной.
, (5.1)