Доказательство

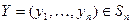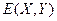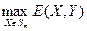Для каждого функция есть непрерывная линейная функция от , определенная на замкнутом подмножестве S_m пространства E^m . Т.е. существует для любого .

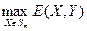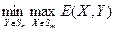В свою очередь, - непрерывная кусочно-линейная функция от . Т.е. существует.

Аналогично показывается существование .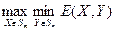

Если первое условие леммы о матрицах выполняется, то существует элемент 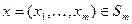такой, что

, т.е. для любого

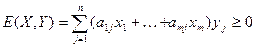. (1)

Так как (1) справедливо для любого , то и, следовательно,

. (2)

Аналогично из второго условия леммы о матрицах

. (3)

Поскольку выполняется либо первое либо второе условие леммы, то по крайней мере одно из (2) и (3) выполняется и, следовательно, неравенство

(4)

не может быть справедливо.

Пусть А_к матрица, полученная вычитанием k из всех элементов А:

.

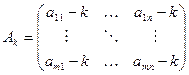Пусть Е_к - математическое ожидание выигрыша для А_к, так что для любого и любого :

. (5)

Тогда точно так же, как мы показали , что (4) неверно для А, можно показать, что

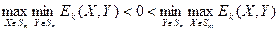(6)

неверно для А_к.

Из (5) легко увидеть:

. (7)

Из (6) и (7) очевидно, что

неверно, т.е.

- неверно.

А поскольку последнее неравенство невернодля любого k, то теперь можно записать:

- неверно.

Тогда справедливо: .

Но по Теореме 1: , т.е.

.

 

Другими словами, основная теорема теории матричных игр утверждает, что каждая матричная игра двух партнеров с нулевой суммой имеет решение, т.е. существуют оптимальные смешанные стратегии X* и Y* для обоих игроков, причем , так что для произвольных смешанных стратегий и :

E(X,Y*)£ E(X*,Y*)£ E(X*,Y).