I. Изображение кривых.

Растр

Вводные понятия

Изображение кривых 1

Лекция 2

 

Под "изображением" какой-либо геометрической фигуры мы будем понимать растеризацию - нахождение максимально точного приближения к изображению данной фигуры на дискретной решетке.

Прежде всего, введем понятие растра:

 

Самое общее определение растра - это множество M, такое, что существует взаимно однозначное (биективное) отображение

, где X Ì Z, Y Ì Z

Если множества X и Y -конечные, то растр будем называть прямоугольным, в противном случае будем называть его бесконечным.

Элементы растра мы будем называть пикселами (англ. pixel - от picture element) и обозначать M_ij=F(i,j). Пиксел может иметь различные атрибуты, но при рассмотрении задач растеризации простейших геометрических объектов будем считать, что у него есть только два состояния: 1 - видимый и 0 - невидимый.

Существует два подхода к определению пикселов:

1. Пикселы - точки с целочисленными координатами

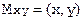
Рис. 1. Растр 5x3 (первый подход).

2. Пикселы - квадраты, лежащие между координатными прямыми с целочисленными координатами

Рис. 2. Растр 5x3 (второй подход).

Мы будем пользоваться первым или вторым подходом в зависимости от того, какой из них будет удобнее в конкретной ситуации.

 

 

Пусть у нас есть некоторая кривая, и мы хотим построить ее изображение на растровой решетке. Возникает вопрос: какие из ближайших пикселов следует закрашивать?

 

Пусть (x0,y0) - наша точка , а (x,y) - некоторая другая точка,

для определения "близких" пикселов введем следующие понятия:

 

1. 4- связность
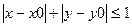
2. 8- связность

 

В дальнейших рассуждениях расстояние будем считать заданным стандартной евклидовой метрикой.