Представление в виде графа
Задача коммивояжёра
Задача коммивояжёра ( англ. Travelling salesman problem, TSP)(коммивояжёр — разъездной сбытовой посредник) — одна из самых известных задач комбинаторной оптимизации, заключающаяся в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется средигамильтоновых циклов.
Существует несколько частных случаев общей постановки задачи, в частности геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.
Общая постановка задачи, впрочем как и большинство её частных случаев, относится к классу NP-полных задач. Задача коммивояжёра относится к числу трансвычислительных: уже при относительно небольшом числе городов (66 и более) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет.
Непременным условием и единственным смыслом задачи коммивояжёра (далее: З.К.) является поиск самого выгодного пути. Для этого необходимо найти и описать все возможные пути при любом из вариантов способов поиска решения. Если мы не просчитали все пути в выбранном варианте решения, то мы не можем утверждать, что найденное решение самое выгодное. Что такое проверка решения? - это поиск ошибки в процессе решения или сверка полученного результата с заведомо правильным. Второй вариант временно отбрасываем, так как нет практического смысла в решении задачи, если уже есть решение (в свою очередь, использование ранее выполненого верного решения для части имеющейся задачи - способ уменьшить решение). В рамках данной работы не ставилось целью сравнение различных методов и способов решения, поэтому принимаем, что проверяющий также считает выбраный способ решения оптимальным и проверяет его на правильность. Что нужно сделать проверяющему? - повторить работу, проделанную при решении, в полном объёме для поиска ошибки на каждом этапе решения. Если будет найдена ошибка, то проверяющему будет необходимо продолжить процесс решения для поиска более выгодного маршрута. Таким образом, мы получаем, что проверка решения З.К. равна или больше самого решения. Следовательно, либо задача относится к P-классу либо NP=P!. Мнение автора статьи, что З.К. - полиномиальная задача в силу своей геометрической специфики. Обобщёная З.К. является подтверждением NP=P!.


Симметричная задача для четырех городов.
Для возможности применения математического аппарата для решения проблемы, ее следует представить в виде математической модели. Проблему коммивояжёра можно представить в виде модели на графе, то есть, используя вершины и ребра между ними. Таким образом, вершины графа (на рис.: От A до D) соответствуют городам, а ребра  между вершинами
между вершинами  и
и  — пути сообщения между этими городами. Каждому ребру
— пути сообщения между этими городами. Каждому ребру  можно сопоставить критерий выгодности маршрута
можно сопоставить критерий выгодности маршрута 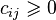 (На рис.: 20, 42, …), который можно понимать как, например, расстояние между городами, время или стоимость поездки. Маршрутом (также гамильтоновым маршрутом) называется маршрут на таком графе, в который входит по одному разу каждая вершина графа. Задача заключается в отыскании кратчайшего маршрута.
(На рис.: 20, 42, …), который можно понимать как, например, расстояние между городами, время или стоимость поездки. Маршрутом (также гамильтоновым маршрутом) называется маршрут на таком графе, в который входит по одному разу каждая вершина графа. Задача заключается в отыскании кратчайшего маршрута.
В целях упрощения задачи и гарантии существования маршрута, обычно считается, что модельный граф задачи является полностью связным, то есть, что между произвольной парой вершин существует ребро. В тех случаях, когда между отдельными городами не существует сообщения, этого можно достичь путем ввода рёбер с максимальной длиной. Из-за большой длины такое ребро никогда не попадет к оптимальному маршруту, если он существует.
В зависимости от того, какой критерий выгодности маршрута сопоставляется величине ребер, различают различные варианты задачи, важнейшими из которых являются симметричная и метрическая задачи.