Жадный алгоритм

Улучшения алгоритма

Сложность QSORT

Один проход алгоритма имеет сложность Ө(n).

В лучшем случае, если на каждом шаге опорные элементы делят массив на две равные половины, сложность алгоритма будет Ө(n log n).

В худшем случае, если опорные элементы будут иметь наименьшие или наибольшие ключи, на каждом проходе число отсортированных элементов будет уменьшаться на 1, понадобится (n-1) проход, и сложность будет Ө(n2).

Можно доказать, что в среднем сложность быстрой сортировки Ө(n logn)

¢ Использование простого алгоритма (вставками) для небольших частей массива (до 10 элементов).

 

procedure QuickSort (l,t:integer);

var i:integer;

begin

if t-l>m then

begin

i:=part(l,t); QuickSort (l,i-1); QuickSort (i+1,t);

end

Else Insertion(l,t);

end;

 

¢ Выбор в качестве опорного случайного элемента, либо медианы из трех: первого, последнего и среднего.

x := a[ l + random (r – l + 1) ]

Жадный алгоритм ( англ. Greedy algorithm) — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным. Известно, что если структура задачи задается матроидом, тогда применение жадного алгоритма выдаст глобальный оптимум.

Если глобальная оптимальность алгоритма имеет место практически всегда, его обычно предпочитают другим методам оптимизации, таким как динамическое программирование.

Матроид — классификация подмножеств некоторого множества, представляющая собой обобщение идеи независимости элементов, аналогично независимости элементов линейного пространства, на произвольное множество.

Условия применимости

Общего критерия оценки применимости жадного алгоритма для решения конкретной задачи не существует, однако, для задач, решаемых жадными алгоритмами, характерны две особенности: во-первых, к ним применимПринцип жадного выбора, а во-вторых, они обладают свойством Оптимальности для подзадач.

[править]Принцип жадного выбора

Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме:

1. Доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадным выбором и не хуже первого.
2. Показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной.
3. Рассуждение завершается по индукции.

[править]Оптимальность для подзадач

Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач. Например, в задаче о выборе заявок можно заметить, что если — оптимальный набор заявок, содержащий заявку номер 1, то — оптимальный набор заявок для меньшего множества заявок , состоящего из тех заявок, для которых .

Примеры Размен монет

[править]

Задача. Монетная система некоторого государства состоит из монет достоинством . Требуется выдать сумму 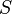наименьшим возможным количеством монет.

Жадный алгоритм решения этой задачи таков. Берётся наибольшее возможное количество монет достоинства : . Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.

Для данной задачи жадный алгоритм не всегда даёт оптимальное решение. Например, сумму в 24 копейки монетами в 1, 5 и 7 коп. жадный алгоритм разменивает так: 7 коп. — 3 шт., 1 коп. — 3 шт., в то время как правильное решение — 7 коп. — 2 шт., 5 коп. — 2 шт. Тем не менее, на всех реальных монетных системах жадный алгоритм даёт правильный ответ.

Выбор заявок

[править]

Формулировка № 1. Даны заявок на проведение занятий в некоторой аудитории. В каждой заявке указаны начало и конец занятия (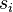 и для -й заявки). В случае пересечения заявок можно удовлетворить лишь одну из них. Заявки с номерами и совместны, если интервалы и не пересекаются (то есть 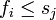или ). Задача о выборе заявок состоит в том, чтобы набрать максимальное количество совместных друг с другом заявок.

Формулировка № 2. На конференции, чтобы отвести больше времени на неформальное общение, различные секции разнесли по разным аудиториям. Учёный с чрезвычайно широкими интересами хочет посетить несколько докладов, проходящих в разных секциях. Известно начало 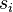и конец каждого доклада. Определить, какое максимальное количество докладов можно посетить.

Приведём жадный алгоритм, решающий данную задачу. При этом полагаем, что заявки упорядочены в порядке возрастания времени окончания. Если это не так, то можно отсортировать их за время ; заявки с одинаковым временем конца располагаем в произвольном порядке.

Activity-Selector(s,f)

1. length[s]
2. 
3. 
4. for to do

if then

1. return A

На вход данному алгоритму подаются массивы начала и окончания занятий. Множество A состоит из номеров выбранных заявок, а j — номер последней заявки. Жадный алгоритм ищет заявку, начинающуюся не ранее окончания j-той, затем найденную заявку включает в A, а j присваивает её номер. Таким образом, каждый раз мы выбираем то (ещё не начавшееся) занятие, до конца которого осталось меньше всего времени.

Алгоритм работает за , то есть сортировка плюс выборка. На каждом шаге выбирается наилучшее решение. Покажем, что в итоге получится оптимум.

Доказательство. Заметим, что все заявки отсортированы по неубыванию времени окончания. Заявка номер 1, очевидно, входит в оптимум (если нет, то заменим самую раннюю заявку в оптимуме на неё, от этого хуже не станет). Выкинув все заявки, противоречащие первой, получим исходную задачу с меньшим количеством заявок. Рассуждая по индукции, аналогичным образом приходим к оптимальному решению.

 

Другие жадные алгоритмы

• Алгоритм Хаффмана (адаптивный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью).
• Алгоритм Краскала (поиск остовного леса минимального веса в графе).
• Алгоритм Прима (поиск остовного дерева минимального веса в связном графе).
• Алгоритм Лин-Кернига (Кластеризация графа).

Обобщением жадных алгоритмов является алгоритм Радо — Эдмондса.

[править]Задачи, в которых жадные алгоритмы не дают оптимального решения

Для ряда задач, относящихся к классу NP, жадные алгоритмы не дают оптимального решения. К ним относятся:

• задача коммивояжера;
• задача минимальной раскраски графа;
• задача разбиения графа на подграфы;
• задача выделения максимальной клики;
• задачи, связанные с составлением расписаний.

Тем не менее, в ряде задач жадные алгоритмы дают неплохие приближённые решения.