Косвенные измерения
Измерения напряжений (токов).
Для измерения тока и напряжения применяют методы непосредственной оценки и сравнения. В лабораторном практикуме по электротехнике используется в основном метод непосредственной оценки.
Для измерения тока амперметр включают последовательно с нагрузкой R1 (в разрыв ветви) (рис. 8.1).
В связи с тем, что сопротивление амперметра RА отлично от нуля, возникает методическая погрешность измерения, обусловленная включением амперметра:
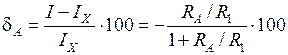
Обычно RА << R1,поэтому  .
.

Рисунок 8.1–Электрическая схема для измерения постоянного тока
Погрешность измерения тока за счет влияния сопротивления амперметра отрицательна, так как показание прибора несколько меньше того значения тока, которое было бы до момента включения прибора в цепь. Следовательно, максимальная погрешность измерения имеет место, если погрешность, определяемая классом точности прибора, также отрицательна.
Для измерения напряжения вольтметр присоединяют параллельно участку цепи, на котором нужно измерить падение напряжения (рис. 8.2).
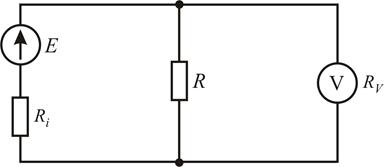
Рисунок 9.2–Электрическая схема для измерения постоянного напряжения
Если к источнику ЭДС Е с внутренним сопротивлением Ri подключить резистор R, то в цепи будет протекать ток 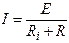 .
.
При этом падение напряжения на резисторе составит U = IR.После подключения вольтметра с входным сопротивлением RV сопротивление внешней цепи (относительно источника энергии) уменьшится. В результате ток в неразветвленном участке цепи увеличится:
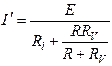 ,
,
причем I > I'. В результате возрастает падение напряжения на внутреннем сопротивлении источника Ri и соответственно уменьшаются падение напряжения на резисторе R и показания вольтметра UV.
Абсолютная методическая погрешность измерения, возникающая за счет шунтирования резистора R сопротивлением RV , равна
 .
.
Относительная методическая погрешность определяется по формуле
 .
.
Очевидно, что абсолютная и относительная методические погрешности измерения будут стремиться к нулю, если  → 0. Поскольку значения Ri и R являются параметрами цепи и остаются неизменными, для уменьшения погрешности входное сопротивление вольтметра
→ 0. Поскольку значения Ri и R являются параметрами цепи и остаются неизменными, для уменьшения погрешности входное сопротивление вольтметра  должно быть как можно больше (в идеале
должно быть как можно больше (в идеале  → ∞). Как указывалось ранее, большим входным сопротивлением обладают электронные вольтметры. Однако и их входное сопротивление Rвх имеет конечное значение, величина которого зависит от предела измерения. Поэтому некоторая малая погрешность δV всегда имеет место.
→ ∞). Как указывалось ранее, большим входным сопротивлением обладают электронные вольтметры. Однако и их входное сопротивление Rвх имеет конечное значение, величина которого зависит от предела измерения. Поэтому некоторая малая погрешность δV всегда имеет место.
Исходя из заданной методической погрешности δV , можноопределить требуемое значение входного сопротивления вольтметра Rвх из выражения:
 .
.
При измерении напряжения переменного тока эквивалентная схема входного сопротивления вольтметра имеет вид, показанный на рис. 8.3.

Рисунок 8.3–Электрическая схема для измерения переменного напряжения
Комплексное входное сопротивление вольтметра:

 .
.
Модуль входного напряжения:
 .
.
Из приведенных выражений следует, что с увеличением частоты входное сопротивление вольтметра уменьшается из-за снижения емкостного сопротивления. В результате возникает дополнительная методическая частотная погрешность вольтметра. В описании прибора указывается значение Rвхи значение Cвх вольтметра для различных пределов измерения. Обычно Rвх =105…108 Ом, Cвх = 30…70 пФ.
Погрешность измерения за счет шунтирующего действия входной цепи вольтметра можно определить, если измеряемую цепь представить схемой (рис. 8.4), состоящей из эквивалентного генератора с ЭДС холостого хода UX, соответствующего измеряемому напряжению и с внутренним сопротивлением Rэкв, соответствующим эквивалентному сопротивлению в точках подключения вольтметра.

Рисунок 8.4–Расчетная схема
Относительную погрешность измерения (в %)можно определить по формуле

На практике при измерениях на частотах меньше 20 кГц частотной погрешностью вольтметра можно пренебречь.
Основная приведенная погрешность зависит от значения измеряемого напряжения. Так, при измерении малых (в пределах 100…300 мВ) напряжений она может достигать 10…15 %, а при измерении больших уровней напряжения – уменьшается в 3–4 раза.
На погрешность измерения (на частотах выше 0,1…0,3 МГц) оказывают влияние индуктивность и активное сопротивление соединительных проводов. Поэтому их длины должны быть по возможности меньшими (до 0,5 м).
При измерении напряжений следует обратить особое внимание на выбор предела измерений (так же, как и при измерении тока).
У электронных вольтметров имеется два входных зажима, к которым подключается измеряемое напряжение U. Один зажим обычно соединен с корпусом прибора, поэтому его называют корпусным и обозначают  . Другой зажим является потенциальным.
. Другой зажим является потенциальным.
Для уменьшения погрешности измерения и влияния помех корпусный зажим вольтметра соединяется с корпусным зажимом генераторов и других приборов (используемых в эксперименте) или присоединяется к точкам цепи, потенциал которых ближе к нулевому. При этом следует избегать касания корпусов приборов.
Таким образом, при измерении напряжений нужно брать приборы с большим внутренним сопротивлением и выбирать пределы измерения так, чтобы при измерении стрелка прибора отклонялась на возможно больший угол.
Измерение мощности. Измерение мощности в цепях постоянного тока, активной и реактивной мощностей в цепях переменного тока (однофазных и трехфазных) промышленной частоты производится обычно электродинамическими и ферродинамическими ваттметрами.
Схема подключения ваттметра PW для измерения в цепях постоянного тока или в однофазной цепи переменного тока приведена на рис. 8.5.

Рисунок 8.5–Электрическая схема для измерения мощности
Такая схема включения обеспечивает минимальную погрешность измерения, когда сопротивление нагрузки намного больше сопротивления токовой катушки ваттметра, что в большинстве случаев имеет место. При этом неподвижная (токовая) катушка ваттметра включается в разрыв цепи, а подвижная катушка (напряжения) подключается параллельно нагрузке.
Начала катушек (генераторные зажимы) обозначаются звездочкой (*) или знаком (+). Эти зажимы должны быть подключены к положительному полюсу источника питания.
В цепях постоянного тока потребляемая нагрузкой мощность определяется произведением тока в нагрузке на падение напряжения на ней: P = UI.
При измерении мощности в однофазной цепи переменного тока показание ваттметра соответствует активной мощности (Вт):
P = UIcosφ,
где U и I – среднеквадратические значения напряжения и тока нагрузки; φ – фазовый сдвиг между током инапряжением.
При этом обмотка напряжения ваттметра включается на фазное напряжение, а обмотка тока включается в рассечку провода фазы.
Реактивная мощность (в варах) в лабораторном эксперименте обычно не измеряется, а определяется из выражения
Q = UIsinφ.
Для нахождения мощности в трехфазной четырехполюсной цепи при несимметричной нагрузке необходимо взять алгебраическую сумму показаний трех ваттметров, включенных в каждую фазу:
Р = РА + РВ + РС .
Электродинамические ваттметры, предназначенные для измерения мощности в цепях постоянного и переменного тока низкой частоты (16…5000 Гц), выпускаются от 0,1 до 2,5 класса точности. Они рассчитаны на непосредственное включение в цепь с напряжением от 15 до 300 В при токе в цепи от 0,25 до 10 А.
При прямых измерениях не всегда удается получить значение всех исследуемых величин (токов, напряжений, мощности, фазы и др.) методом прямого измерения. Это обусловливается отсутствием специальных приборов прямого измерения или невозможностью подключения прибора к некоторым элементам цепи и другими причинами.
Кроме того, не всегда целесообразно производить непосредственное измерение всех интересующих величин, если они могут быть получены с достаточной точностью из функциональных зависимостей, связывающих их с измеряемыми величинами. Это позволяет проводить эксперимент быстрее и с меньшими аппаратурными затратами за счет уменьшения числа измерений.
Измерение тока с помощью электронных вольтметров. Косвенный метод измерения тока с помощью электронного вольтметра заключается в следующем. В ветвь, в которой необходимо измерить ток, последовательно с нагрузкой включают образцовый резистор R0. Падение напряжения на этом резисторе измеряют с помощью электронного вольтметра, так как он работает в широком диапазоне частот и потребляет от измеряемой цепи малую мощность, что способствует обеспечению минимума методической погрешности.
Ток, текущий через резистор R0, а следовательно, и по всей цепи (рис. 8.6), определяется законом Ома:  , где U0 – показание вольтметра, включенного параллельно резистору R0.
, где U0 – показание вольтметра, включенного параллельно резистору R0.

Рисунок 8.6–Измерение тока с помощью электронного вольтметра
Включать резистор R0следует в разрыв проводника, идущего от корпуса генератора.
В этом случае корпусная точка измерительного прибора соединяется с корпусом генератора, что обеспечивает меньшее влияние помех и стабильность работы вольтметра. Минимум методической погрешности обеспечивается при правильном выборе сопротивления резистора R0. Чем меньше сопротивление R0, тем меньше оно оказывает влияние на ток, протекающий в искомой ветви.
С другой стороны, чем меньше падение напряжения на резисторе, тем труднее его точно измерить, поскольку больше сказывается влияние различных наводок, увеличение погрешности вольтметра на малых пределах измерения. Поэтому сопротивление R0, а, следовательно, падение напряжения на нем должны быть наибольшими. В этом случае принимают компромиссное решение, выбирая сопротивление R0 по условию: R0 < 0,1ZН, здесь ZН– модуль сопротивления ветви в том месте, где измеряется ток. В этом случае ток в ветви при включении резистора R0изменится незначительно. Значение сопротивления цепи ZН можно определить с помощью приближенного предварительного расчета или экспериментально. В лабораторных стендах имеются эталонные резисторы, сопротивление которых составляет 1 Ом, или любые другие, набранные с помощью магазинов сопротивления. Для этих целей можно использовать также резисторы цепи с известным сопротивлением.
Косвенный метод измерения тока наиболее широко применяется в цепях переменного тока с частотой от 500 Гц до 10 МГц.
Измерение мощности. Сущность косвенного измерения мощности в цепях постоянного тока заключается в измерении с помощью вольтметра и амперметра напряжения U и тока I цепи, в вычислении мощности по ранее приведенной формуле P = UI.
Анализ показывает, что погрешность измерения мощности будет минимальной при включении измерительных приборов по схеме, приведенной на рис. 8.7,а, если выполняется условие
 ,
,
где  – сопротивление нагрузки; RА – сопротивление амперметра;
– сопротивление нагрузки; RА – сопротивление амперметра;  – сопротивление вольтметра, или по схеме рис. 8.7,б при условии
– сопротивление вольтметра, или по схеме рис. 8.7,б при условии
 .
.


а) б)
Рисунок 8.7–Электрическая схема для измерения мощности
косвенными методами
Учитывая, что RV является весьма большим, а RА – весьма малым, можно считать I ≈ Iн, U ≈ Uн.
Для известного сопротивления нагрузки Rн потребляемая им мощность определяется из выражения P= I 2Rн.
Для измерения мощности косвенным методом в цепях переменного тока применяются амперметр, вольтметр и фазометр. При этом активная мощность Р определяется по формуле  .
.
Если прямым методом измерены значения напряжения U, тока I и мощности P, величина cosφ определяется расчетным путем: сosφ = 
Измерение параметров электрической цепи R, С, L, Z.Основными элементами электрической цепи с сосредоточенными параметрами являются: резистор, конденсатор, катушка индуктивности. Им соответствуют основные параметры: активное сопротивление электрическому току R, емкость С, индуктивность L.
Метод амперметра-вольтметра. Этот метод основан на раздельном измерении тока I в цепи измеряемого сопротивления RХ и напряжения U на его зажимах и на последующем вычислении значения RХ по показаниям измерительных приборов:
RХ =  .
.
При измерении малых сопротивлений порядка 0,01…100 Ом постоянному току применяют схему, показанную на рис. 8.8,а. С помощью реостата R1 устанавливают приемлемое значение тока в цепи.

а)

б)
Рисунок 8.8–Измерение параметров электрической цепи
В схеме (см. рис. 8.8,а) вольтметр показывает значение напряжения на зажимах RХ (U = UХ ), амперметр – сумму токов IА = IV + I, следовательно
 ,
,
где IV – ток, проходящий через вольтметр; RV – внутреннее (входное) сопротивление вольтметра
RV >>RX, то RХ ≈ .
.
Абсолютная методическая погрешность ΔRХ определяется по формуле
 ,
,
а относительная погрешность (в %)
 .
.
Для измерения больших сопротивлений (до сотен кОм и более) применяют схему (рис. 8.8,б), где амперметр регистрирует значение тока в цепи RХ (I = IА), а вольтметр – сумму падений напряжений (U + UA).
По показаниям приборов можно вычислить результат измерения
 ,
,
где RА – внутреннее сопротивление амперметра.
Абсолютная погрешность  и относительная (в %)
и относительная (в %)  .
.
Учитывая, что RА << RX, можно считать U ≈ UV .
Нужно иметь в виду, что погрешность измерения методом вольтметра и амперметра всегда больше суммы приведенных погрешностей используемых приборов. Однако, считая, что знак погрешностей измерения известен, их можно всегда учесть.
Метод амперметра-вольтметра можно применять для измерения на переменном токе модуля полного сопротивления цепи ZХ по схеме, представленной на рис. 8.9.

Рисунок 8.9–Электрическая схема для измерения модуля полного сопротивления цепи
 В этом случае
В этом случае
 ,
,
где R, X – соответственно активная и реактивная составляющие сопротивления.
Для обеспечения минимальной погрешности измерения входное сопротивление вольтметра на частоте измерения должно удовлетворять условию Zвх >> ZХ.
Из предыдущего выражения следует, что метод амперметра-вольтметра можно применять для измерения активного сопротивления резистора переменному току R, когда его индуктивными и емкостными составляющими сопротивления можно пренебречь; а также для измерения индуктивности L катушки и емкости С конденсатора, отличающихся высокой добротностью (т.е. когда активное сопротивление катушки RL чрезвычайно мало, а сопротивление изоляции конденсатора весьма велико).
В этом случае
 ,
,  ,
,
где f – частота питающего напряжения.
Литература
1. Сергеев А.Г., Крохин В.В. Метрология: Учеб. Пособие для вузов. – М.: Логос, 2001. – 408 с
2. Зайдель А. Н. Погрешности измерения физических величин. Л.: Наука, 1985.- 112 с.
3. Бурдун Г.Д., Марков Б.Н. Основы метрологии. – М.: Издательство стандартов, 1975.
4. Тюрин Н.И. Введение в метрологию. – М.: Изд-во стандартов, 1976.
5. ГОСТ 16263-70 Государственная система обеспечения единства измерений. Метрология. Термины и определения.
6. Сена Л.Г. Единицы физических величин и их размерности. – М.: Наука, 1969.
7. Сергеев А.Г., Латышев М.В., Терегеря В.В. Метрология, стандартизация, сертификация: Уч. пос. — М.: Логос, 2003.- 536 с.