Разложение в ряд Фурье.
Периодические сигналы можно представить в виде суммы гармонических функций либо комплексных экспонент с частотами, образующими арифметическую прогрессию.
Для того чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:
– не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции);
– число разрывов первого рода должно быть конечным;
– число экстремумов должно быть конечно (в качестве примера функции, не удовлетворяющей этому условию можно привести функцию  в окрестности нуля).
в окрестности нуля).
Существует несколько форм записи ряда Фурье.
Синусно-косинусная форма.
 , (11)
, (11)
где  ,
,  - кратная частота, называемая гармоникой.
- кратная частота, называемая гармоникой.
Коэффициенты ряда  ,
,  и
и  рассчитываются по формулам:
рассчитываются по формулам:
 ;
;  ;
;  .
.
Если 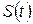 - четная функция,
- четная функция,  ,
, 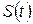 - нечетная –
- нечетная –  .
.
Вещественная форма.
 . (12)
. (12)
Для четной функции 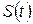
 и
и  , для нечетной –
, для нечетной –  .
.
Комплексная форма:
 . (13)
. (13)
Комплексные коэффициенты ряда связаны с вещественными следующими соотношениями:
 ,
,  ,
,  .
.
Связь с синусно-косинусной формой:
 ,
,  ,
,  . (14)
. (14)
Расчет коэффициентов 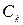 ряда Фурье в комплексной форме:
ряда Фурье в комплексной форме:
 . (15)
. (15)
Если 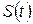 – четная, то
– четная, то 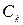 - вещественные, если нечетная – мнимые.
- вещественные, если нечетная – мнимые.
Совокупность амплитуд гармоник ряда Фурье называется амплитудным спектром, а совокупность их фаз – фазовым спектром.
Если анализируемый сигнал 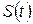 является вещественным, то его амплитудный и фазовый спектры обладают симметрией:
является вещественным, то его амплитудный и фазовый спектры обладают симметрией:
 ;
;  ;
;  . (16)
. (16)