Элементы теории статистических решений

Функционирование больших систем происходит в условиях, когда параметры среды заранее неизвестны. Это обстоятельство вызывает неопределенность при выборе рациональных параметров систем. Например, случайными могут быть такие параметры среды, как рельеф местности, метеоусловия, уровень радиации, действия противника и т. п. В отличие от игровой ситуации, когда противоположная система разумно противодействует системе, принимающей решение, среда или природа изменяют свои параметры случайно, не преследуя собственных целей.

Математический аппарат, предназначенный для принятия решений в игровых ситуациях, в которых одна из систем случайно выбирает стратегию, называется теорией статистических решений.

Теория статистических решений оперирует играми, в которых внешняя среда или природа рассматриваются как противоположные системы. Рассмотрим модель игровой ситуации.

Система 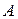, принимающая решение, имеет множество стратегий . Среда может принимать конечное множество состояний . Вероятности состояний среды могут быть заданы в виде вектора или неизвестны. Задана матрица . Каждый элемент матрицы представляет полезность стратегии при состоянии среды .

Требуется определить такую стратегию , которая является предпочтительной в некотором смысле по сравнению с другими.

Таблица 8.3. Платежная матрица

 

			……
			……
			……
………………………….	……	……	……	……
			……

 

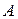
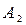
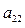
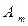
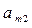
Для решения поставленной задачи следует исключить дублирующие и заведомо невыгодные стратегии системы . Для среды этого делать не следует, так как выбор ее стратегии производится случайно.

В теории статистических решений наряду с платежной матрицей (табл. 8.3) пользуются матрицей рисков. Риском называется разность между максимально возможным выигрышем при состоянии среды и выигрышем при выборе конкретной стратегии . Обозначив максимальный элемент столбца платежной матрицы

^, (8.20)

согласно определению получим

(8.21)

Матрица рисков эквивалентна платежной матрице .

Выбор предпочтительной стратегии системы может производиться в двух различных ситуациях.

1. Вероятности состояния среды заданы в виде вектора

.

В этом случае в качестве показателя эффективности выбирают среднее значение, или математическое ожидание выигрыша системы :

. (8.22)

Предпочтительной будет стратегия , при которой максимизируется средний выигрыш:

. (8.31)

Если используется матрица рисков, то соответственно

; (8.24)

. (8.25)

2. Вероятности состояния среды неизвестны. Существуют несколько критериев для определения предпочтительной стратегии системы .

Критерий Вальда (критерий крайнего пессимизма) совпадает с критерием выбора стратегии, позволяющим получить нижнюю цену парной игры:

. (8.26)

Критерий минимального риска Севиджа рекомендует выбирать стратегию, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации:

. (8.27)

Критерий Гурвица учитывает как пессимистический, так и оптимистический подходы к оценке ситуации:

, (8.28)

где .

Выбор критерия принятия решения является наиболее сложным и ответственным этапом, для которого не существует каких – либо общих рекомендаций. Выбор критерия производит руководитель системы с учетом специфики задачи и целей системы. В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если, наоборот, определенный риск вполне приемлем и в систему вложены средства, то выбирают критерий Севиджа. При отсутствии достаточной информации для выбора того или иного критерия возможен альтернативный подход, который связан с вычислением шансов на выигрыш на основе прошлого опыта.

 

Вопросы для самопроверки по разделу 8

1. Что такое игра в терминах теории игр?

2. Какая игра называется конечной?

3. В чем заключается решение игры в теории игр?

4. Как определяется верхняя цена игры?

5. Как определяется минимаксная стратегия игры?

6. Какие границы имеет выигрыш системы?

7. В каких пределах лежит фактический результат игры (цена игры)?

8. Что такое платежная матрица?

9. Как называется седловая точка платежной функции?

10. По каким правилам происходит переход от исходной задачи к симметричной двойственной?

11. Являются ли симметричные двойственные задачи взаимно двойственными?

12. Что такое взаимная двойственность?

13. Что называется теорией статистических решений?

14. Как строится матрица рисков?

15. Что такое риск в теории игр?

16. Какие критерии для определения предпочтительной стратегии вы знаете?

17. Какой критерий позволяет получить нижнюю цену парной игры?

18. Что такое минимаксная и максиминная стратегии?

19. Дайте определение оптимальных стратегий.

20. В чем суть метода Брауна?

21. Сформулируйте критерий Вальда.

22. Сформулируйте критерий Севиджа.

23. Сформулируйте критерий Гурвица.

 

заключение

 

Математические методы системного анализа и теории принятия решений, рассмотренные в данном курсе, сегодня являются необходимым инструментарием менеджера-аналитика. Они составляют необходимую часть системного анализа и активно используются в исследовательской практике организаций и предприятий различной направленности и структуры.

Их знание и использование широко применяются при отображении и моделировании реальных процессов и явлений, изначально имеющих динамику развития.