Сведения игровой задачи к задаче линейного программирования

Решение игровых задач с помощью линейного программирования

В матричных играх число существенных стратегий каждой системы превышает две. Для решения игры , то есть нахождения упорядоченной пары оптимальных смешанных стратегий, воспользуемся свойствами оптимальных смешанных стратегий (8.9) и (8.10). Примем следующие допущения:

- каждая система пользуется своей оптимальной смешанной стратегией;

- коэффициенты игровой матрицы .

Если система 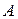использует оптимальную смешанную стратегию , то при любой системы ее проигрыш будет не меньше цены игры. Действительно, если система применит существенную стратегию, то на основании выражения (8.10) ее проигрыш будет равен цене игры. Несущественная стратегия системы приведет к проигрышу, большему, чем цена игры.

Поэтому любая стратегия вызовет проигрыш, равный

. (8.4)

К полученной системе неравенств следует добавить нормировочное условие

. (8.5)

Поделим левые и правые части выражений (8.5) и (8.4) на :

; (8.6)

(8.7)

и введем обозначение . Так как система 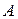стремится максимизировать выигрыш, то она выберет такие составляющие смешанной стратегии (соответственно ), которые обеспечат или . Рассматривая как целевую функцию, выражения (8.6) и (8.7) представим в виде задачи линейного программирования:

; (8.8)

; (8.9)

.

Для определения оптимальной смешанной стратегии системы будем исходить из предположения, что любая (существенная или несущественная) стратегия системы 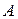обеспечит ей выигрыш, не больший цены игры:

. (8.10)

Нормировочное условие для стратегий системы имеет вид

. (8.11)

Поделим левые и правые части выражений (8.11) и (8.10) на :

; (8.12)

(8.13)

и введем обозначение .

Так как система стремится минимизировать свой проигрыш, то она выберет такие составляющие смешанной стратегии (соответственно ), которые обеспечат или . Рассматривая как целевую функцию, выражения (8.12) и (8.13) представим в виде задачи линейного программирования:

; (8.14)

; (8.15)

.

Таким образом, игра сведена к паре задач линейного программирования, называемых симметричными двойственными. Задача (8.8) – (8.9) получила название исходной, а задача (8.14) – (8.15) – двойственной. В линейном программировании исходная задача имеет вид

; (8.16)

;

;

;

.

 

Двойственная симметричная задача к задаче (8.16) имеет вид

; (8.17)

;

;

;

.

Переход от исходной задачи к симметричной двойственной производится по следующим правилам:

1) вместо задачи максимизации имеем задачу минимизации и наоборот;

2) неравенства в ограничениях заменяем на противоположные;

3) коэффициентами целевой функции двойственной задачи становятся константы ограничений исходной задачи;

4) константами ограничений двойственной задачи становятся коэффициенты целевой функции исходной задачи;

5) матрица коэффициентов ограничений транспонируется.

Симметричные двойственные задачи взаимно двойственны, то есть задача, двойственная к двойственной, является исходной. Двойственные задачи, к которым сведена игра , получаются из задач (8.16) и (8.17) делением каждого ограничения в задачах (8.16) и (8.17) на свою константу с переобозначением коэффициентов ограничений. Так как каждая задача линейного программирования имеет двойственную задачу и каждая матричная игра сводится к паре двойственных задач линейного программирования, то можно утверждать, что задаче линейного программирования может соответствовать матричная игра.

Матричная игра в соответствии с основной теоремой всегда имеет решение, следовательно, линейные двойственные задачи (8.8) – (8.9) и (8.14) – (8.15) всегда разрешимы. Обратное утверждение неверно, так как не всякая задача линейного программирования разрешима. Значит, матричная игра соответствует разрешимой задаче линейного программирования, неразрешимой же задаче не соответствует никакая игра.

В теории линейного программирования доказано, что оптимальные решения пары двойственных задач обусловливают одно и то же значение целевой функции. Отсюда следует, что цена матричной игры равна

, (8.18)

где – оптимальные решения двойственных задач (8.8) – (8.9) и (8.14) – (8.15).

Составляющие оптимальных стратегий и определяют из соотношений

. (8.19)

; .