Графическое решение игр (2 x n) и (m x 2)

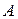Математическая модель конечной парной игры с нулевой суммой представляет собой так называемую платежную матрицу размера , где – число стратегий системы ; – число стратегий системы . Элемент матрицы представляет собой выигрыш системы 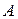, если она применяет стратегию 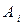, а система использует стратегию .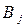

Если каждая из систем выбирает однозначно с вероятностью 1 некоторую стратегию, то решение игры будет в чистых стратегиях. Оптимальное решение игры соответствует максимально возможному выигрышу системы 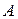(минимально возможному проигрышу системы ). Таким образом, решение игры заключается в нахождении оптимальных чистых стратегий систем.

 

Таблица 8.2. Платежная матрица размера

 

			……
			……
			……
………………………….	……	……	……	……
			……

 

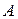
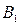
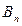
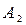
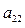
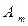
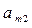
Пусть система 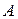выбирает стратегию 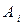. Так как система стремится минимизировать свой проигрыш, то она выберет стратегию 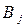, при которой выигрыш системы 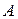минимален. Минимальный выигрыш системы 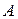при выборе стратегии 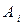будет

.

Чтобы обеспечить себе максимальный выигрыш, система 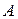должна выбирать такую стратегию , при которой ее минимальный выигрыш максимален:

. (8.1)

Величина 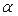называется нижней ценой игры и представляет собой гарантированный выигрыш системы 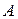. Стратегия, обеспечивающая системе 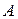получение 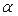, называется максиминной.

Аналогично система при выборе стратегии 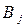будет иметь проигрыш

,

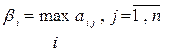так как система 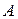выберет стратегию 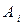, при которой проигрыш системы максимален. Следовательно, оптимальной для системы будет та стратегия , при которой ее максимальный проигрыш минимален:

. (8.2)

Величина называется верхней ценой игры, а соотвтствующая проигрышу стратегия системы - минимаксной.

Таким образом, выигрыш системы 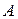или проигрыш системы при выборе ими оптимальных стратегий не может быть больше верхней цены игры и не может быть меньше нижней цены игры. Фактический результат игры, называемый ценой игры, лежит в пределах

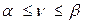(8.3)