Мгновенная поставка, возникновение дефицита допускается

Однокаскадные СУЗ при вероятностном спросе

График измене­ния текущего объема запа­са показан на рис. 7.6, где y₁ – максимальный уровень запаса, Т₁ – период пополнения.

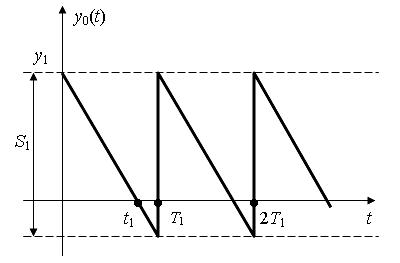
Рис.7.6. График измене­ния текущего объема запа­са

 

Начальный запас в каждом пе­риоде будет исчерпан к моменту времени t₁, то есть .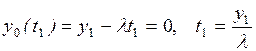

На интервале [0, t] y₀(t)>0 и имеют место издержки хранения:

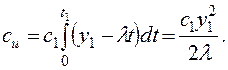
На интервале [t₁, T₁] y₀(t)<0 имеет место дефицит и склад выплачивает штраф в размере

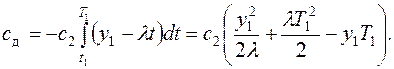
Знак «минус» перед интегралом учитывает, что дефицит равен объему запаса с противоположным знаком.

Функция затрат в единицу времени

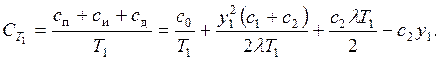(7.7)

Для определения оптимальных параметров стратегии управления запасами приравниваем производные функции (7.7) по у₁ и T₁к нулю, то есть

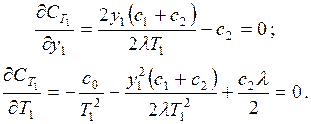
Из первого уравнения находим:

(7.8)

и, подставляя его во второе уравнение, получим

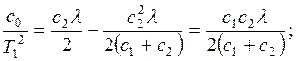
(5.9)

Подставляя выражение (7.9) в уравнение (7.8), находим:

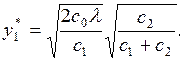(5.10)

Из формулы (7.7) с учетом выражений (7.9) и (7.10) находим минимальные затраты в единицу времени на пополнение, хранение запасов и выплату штрафов:

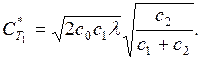(5.11)

Из выражений (7.9) – (7.11) и формул Уилсона (7.5) и (7.6) следует, что задалживание спроса (то есть ликвидация недостач пу­тем накопления требований до очередной поставки и выплаты штрафов) позволяет в 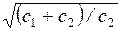раз уменьшить максимальный уровень запаса, минимальное значение функции затрат и частоту заказов (увеличить период пополнения) по сравнению со случаем отсутствия дефицита. Если c₂>>c₁, то 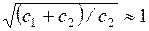и формулы (7.9) – (7.11) совпадают с формулами Уилсона.

Объем заказа при наличии дефицита

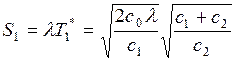(7.12)

превышает объем заказа при отсутствии дефицита в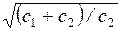раз.

При фиксированной задержке на время t заказ подается в мо­мент t₃ снижения объема запаса до уровня

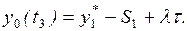
Учитывая выражения (5.10) и (5.12), находим:

Если t = 0, то в момент подачи заказа на складе имеет место максимальный дефицит объемом 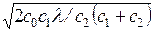.