Векторы и координаты

1) векторы на плоскости:

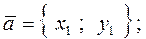
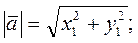
скалярное произведение: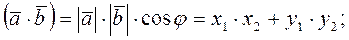

признак коллинеарности: или

признак перпендикулярности: x₁∙x₂ + y₁∙y₂ = 0 ;

 

2) векторы в пространстве:

 

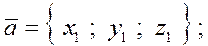
скалярное произведение:

признак коллинеарности: или

признак перпендикулярности: x₁∙x₂ + y₁∙y₂ + z₁∙z₂ = 0 ;

признак компланарности трёх векторов:

x₁ y₁ z₁

x₂ y₂ z₂ = 0 ;

x₃ y₃ z₃

 

векторное произведение двух векторов:

i j k

= x₁ y₁ z₁ ; = S_{параллелограмма} = 2∙S_Δ;

x₂ y₂ z₂

 

смешанное произведение трёх векторов:

x₁ y₁ z₁

= = x₂ y₂ z₂ ;

x₃ y₃ z₃

 

объём параллелепипеда: V_парал = ││ ;

объём пирамиды: V_пирам = V_парал = ││ ;

3) аналитическая геометрия на плоскости:

 

расстояние между двумя точками M₁(x₁ ; y₁) и M₂(x₂ ; y₂)

;

 

уравнение прямой, проходящей через две точки M₁(x₁ ; y₁) и M₂(x₂ ; y₂)

;

 

деление отрезка M₁M₂ в данном отношении λ

 

координаты середины отрезка (M₁M = MM₂ , т.е. λ = 1)

 

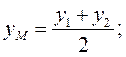
уравнение прямой, проходящей через точку M₀(x₀ ; y₀) перпендикулярно

вектору ()

A∙(x – x₀) + B∙(y – y₀) = 0 ;

 

уравнение прямой с угловым коэффициентом k и проходящей через

точку M₀(x₀ ; y₀)

y – y₀ = k∙(x – x₀) ;

 

острый угол между двумя прямыми y = k₁∙x + b₁ и y = k₂∙x + b₂

условие параллельности двух прямых: k₁ = k₂ ;

 

условие перпендикулярности двух прямых: k₁∙k₂ = −1 ;

 

расстояние от точки M₀(x₀ ; y₀) до прямой A∙x + B∙y + C = 0

 

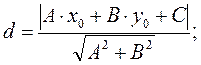
площадь треугольника с вершинами A(x₁ ; y₁) , B(x₂ ; y₂) , C(x₃ ; y₃)

или в другом виде то же самое

x₁ y₁ 1

S_∆ABC = , где D = x₂ y₂ 1 ;

x₃ y₃ 1

 

уравнение окружности радиуса R

(x – a)² + (y – b)² = R² ; центр в точке A(a ; b)

x² + y² = R² ; центр в точке O(0 ; 0)

 

4) аналитическая геометрия в пространстве:

 

расстояние между двумя точками M₁(x₁ ; y₁ ; z₁) и M₂(x₂ ; y₂ ; z₂)

;

 

уравнение прямой в каноническом виде, проходящей через две точки

M₁(x₁ ; y₁ ; z₁) и M₂(x₂ ; y₂ ; z₂)

;

 

деление отрезка M₁M₂ в данном отношении λ

 

координаты середины отрезка (M₁M = MM₂ , т.е. λ = 1)

 

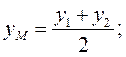
уравнение плоскости, проходящей через точку M₀(x₀ ; y₀ ; z₀)

перпендикулярно вектору

()

 

A∙(x – x₀) + B∙(y – y₀) + C∙(z – z₀) = 0 ;

 

расстояние от точки M₀(x₀ ; y₀ ; z₀) до плоскости A∙x + B∙y + C∙z + D = 0

 

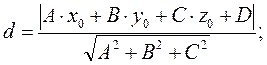
уравнение плоскости, проходящей через три заданные точки

M₁(x₁ ; y₁ ; z₁) , M₂(x₂ ; y₂ ; z₂) , M₃(x₃ ; y₃ ; z₃) :

x – x₁ y – y₁ z – z₁

x₂ – x₁ y₂ – y₁ z₂ – z₁ = 0 ;

x₃ – x₁ y₃ – y₁ z₃ – z₁

 

уравнение сферы радиуса R

(x – a)² + (y – b)² + (z – )² = R² ; центр в точке A(a ; b ; c)

x² + y² + z² = R² ; центр в точке O(0 ; 0 ; 0)