Вычисление бесконечных сумм

End.

Begin

Begin

writeln('введите x и количество слагаемых');

readln(x, k);

s:=0;

a:=1;

b:=sqr(sqr((x+1)));

c:=2*3;

for n:=3 to k+1 do

s:=s+a*(b/c)*sin(Pi/(n-1));

a:=a*(-1);

b:=b*(x+1);

с:=с*(2*n-1)*(2*n-2);

end;

writeln('S=',s:8:5);

 

 

Общая формулировка задач рекуррентного вычисления суммы бесконечного количества элементов:

,

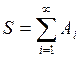где 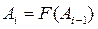, т. е. последующее значение элемента А вычисляется на основе предыдущего его значения. Вычисление продолжается до тех пор, пока разница между предыдущим и последующим значением суммы не станет меньше, чем заданное пользователем значение точности:

.

 

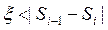В остальном постановка этой задачи аналогична постановке задачи нахождения суммы конечного количества элементов.

 

Общую методологию решения подобных задач рассмотрим на следующем примере:

Необходимо вычислить значение :

 

(2)

 

Вначале, как и в случае с задачей вычисления суммы конечного количества элементов, разобьём исходную формулу суммы на несколько частей (рис. 9).

 

b

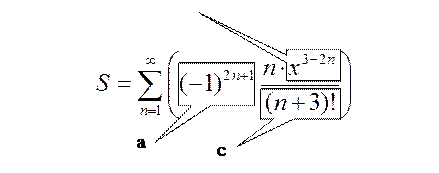
Рисунок 9 – Разбиение элемента суммы формулы 2

 

Элемент n можно вычислить без использования рекуррентной формулы, поэтому для него отдельной переменной не выделено.

Затем сведём в таблицу значения каждой из частей формулы при разных значениях переменной n (см. таблицу 7).

 

Таблица 7 – Изменения частей элемента формулы 2

n	a	b	c
	-1	x1	4! = 1*2*3*4
	-1	x-1	5! = 1*2*3*4*5
	-1	x-3	6! = 1*2*3*4*5*6

 

 

Из таблицы 7 видно, что значение переменной а неизменно, поэтому от её использования можно отказаться. Составим рекуррентные формулы для оставшихся переменных:

 

Рассмотрим подробнее рекуррентное выражение для переменной с. Если обратиться к таблице 7, то можно заметить, что последующее значение переменной с получается домножением предыдущего значения на одно число. При n = 2 необходимо домножить на 5, при n = 3 необходимо домножить на 6.

Это число зависит от числа n, оно соответствует формуле элемента суммы, связанного с переменной с – n+3 (см. рис. 9).

После составления рекуррентных формул можем перейти к составлению алгоритма и программы.

 

 

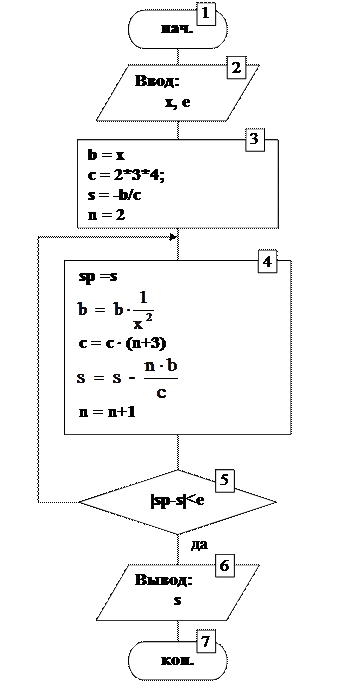
Рисунок 10 – Блок-схема алгоритма вычисления

суммы конечного количества элементов

 

Блок 3 (рис. 10) предназначен для инициализации переменных a и b. В качестве начальных значений используем значения из первой строки таблицы 7 (при n = 2). Затем в этом же блоке вычисляется и сохраняется в переменной s первый элемент суммы, вычисляемый при n = 1.

Цикл repeat не использует переменную счётчик, поэтому вводим её самостоятельно (переменная n). Инициализируется эта переменная также в блоке 3. Её начальное значение - 2, т. к. первый элемент суммы уже вычислен и сохранён до начала цикла.

В теле цикла (блок 4) сначала сохраняем значение переменной s в переменной sp, затем вычисляем новые значения переменных a и b, добавляем к переменной s новый элемент суммы и увеличиваем значение счётчика n.

Теперь в переменной s находится последующее значение суммы , а в переменной sp – предыдущее.Заголовок цикла repeat (блок 5) проверяет условие окончания цикла на основе этих значений и при истинности условия передаёт управление на блок вывода результатов 6.

Теперь можно перейти к реализации алгоритма в исходном тексте программы на языке Pascal.

 

 

program B_S;

var x,s,c,e,sp:real;

n,b:integer;