Рекуррентные вычисления
Begin
Begin
Begin
Temp1 := Expr1;
Temp2 := Expr2;
if Temp1 <= Temp2 then
V := Temp1;
Оператор;
while V <> Temp2 do
V := Succ(V);
Оператор;
end;
end;
end;
Следует обратить внимание на следующее:
Условием выхода из цикла является ложное значение выражения V <> Temp2,и если оператор, содержащийся в теле оператора for, изменяет значение управляющей переменной, то может возникнуть ситуация, когда значение переменной V никогда не станет равным значению Temp2, и цикл не сможет корректно завершиться.
Общая формулировка задач рекуррентного вычисления суммы или произведения конечного количества элементов выглядит следующим образом:
, или 
,
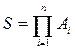где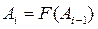 
, т. е. последующее значение элемента А вычисляется на основе предыдущего его значения.
Кроме того, и вычисление суммы, или произведения, можно считать рекуррентным, поскольку следующее значение суммы, или произведения, вычисляется как:
.
Общую методологию решения подобных задач рассмотрим на следующем примере. Необходимо вычислить значение 
:
(1)
Вначале, для упрощения рекуррентной формулы вычисления элемента суммы, разобьём его на несколько частей (рис. 7).
Рисунок 7 – Разбиение элемента суммы формулы 1
Элемент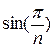 
можно вычислить без использования рекуррентной формулы, поэтому для него отдельной переменной не выделено.
Затем сведём в таблицу значения каждой из частей формулы при разных значениях переменной n (см. таблицу 6).
Таблица 6 – Изменения частей элемента суммы формулы 1
| n | a | b | c |
| (x+1)4 | 3!=1*2*3 | ||
| -1 | (x+1)5 | 5!=1*2*3*4*5 | |
| (x+1)6 | 7!=1*2*3*4*5*6*7 |
Теперь, когда появилась возможность сравнить предыдущее значение части элемента суммы с его последующим значением, можно составить рекуррентные формулы:
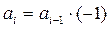
Рассмотрим подробнее рекуррентное выражение для переменной с. Если обратиться к таблице 6, то можно заметить, что последующее значение переменной с получается домножением предыдущего значения на два числа. При n = 3 необходимо домножить на 4 и 5, при n = 4 необходимо домножить на 6 и 7.
Эти два числа определённым образом зависят от числа n. Второе из них соответствует формуле элемента суммы, связанного с переменной с - 2n-1 (см. рис. 7). Тогда первое число можно получить, отняв от числа 2n-1 единицу (поскольку это предыдущее целое число). Откуда и получаем значение 2n-2.
После составления рекуррентных формул можем перейти к составлению алгоритма и программы.
Следует обратить внимание на блок 3 (рис. 8), в котором инициализируются переменные a, b, c. В качестве начальных значений используем значения из первой строки таблицы 6 (при n = 2).
Теперь обратимся к блоку 4. Почему начальное и конечное значения цикла выбраны именно таким образом?
Дело в том, что в блоке 5 вначале выполняется вычисление следующего значения суммы (переменная S), а только затем, с помощью составленных ранее рекуррентных выражений, вычисляются следующие значения переменных a, b и c.
Новые значения переменных a, b и c должны вычисляться при n = 3 (следующее значение), а значение S при n = 2. И если цикл начнётся со значения n = 3, то следующие значения переменных a, b и c будут вычислены правильно, а выражение для вычисления S нужно будет изменить, уменьшив на единицу все вхождения в него переменной n (сравните формулы вычисления переменной S на рисунке 7 и в блоке 5 на рисунке 8).
Рисунок 8 – Блок-схема алгоритма вычисления
суммы конечного количества элементов
Кроме того, чтобы сохранить требуемое количество повторений тела цикла (k-2), увеличим конечное значение счетчика цикла на единицу. Таким образом, количество повторений будет равно: 3–(k+1) = k-2.
Теперь можно перейти к реализации алгоритма в исходном тексте программы на языке Pascal.
program K_S;
var x,s,a,c:real;
n,b:integer;