Показатели вариации
Средние величины, характеризуя вариационный ряд одним числом, не учитывают степень вариации признака.
Для ее измерения используют показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации (R)
.
Среднее линейное отклонение (Д) представляет собой среднюю арифметическую из абсолютных значений отклонений вариантов от средней.
Рассчитывают:
простое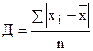 
,
взвешенное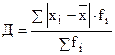 
.
Дисперсия (
) наиболее часто используемый показатель вариации, показывает среднюю площадь отклонений вариантов признака от средней величины.
простая 
,
взвешенная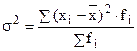 
.
Преобразовав указанные формулы определения дисперсии, можно получить упрощенный вариант формулы (дисперсия методом моментов)
.
Среднее квадратическое отклонение (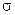
) определяется как квадратный корень из дисперсии.
.
Достоинство среднего квадратического отклонения по сравнению со средним линейным отклонением в том, что при его вычислении никакого условного допущения о необходимости суммирования отклонений вариантов от средней без учета их знаков не делается.
Для сравнения степени вариации признака в разных совокупностях используется коэффициент вариации (ν):
.
Коэффициент вариации может также использоваться для характеристики степени однородности исследуемой совокупности. Вариация признака определяется не только для количественных, но и для качественных признаков, представленных альтернативным признаком:
Дисперсия альтернативного признака равна
,
где p – доля единиц совокупности обладающих изучаемым признаком; g – доля единиц совокупности, не обладающих изучаемым признаком. p+g=1.
В аналитической группировке для изучения вариации результативного признака определяются следующие виды дисперсий:
Внутригрупповая дисперсия (
) показывает вариацию результативного признака в каждой группе, выделенной по факторному признаку
,
где х – варианты результативного признака; 
- среднее значение признака по группе факторного признака; 
- частота признака в каждой группе.
Межгрупповая дисперсия (
) показывает вариацию групповых средних () от средней по всей совокупности (
)
,
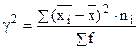где 
- количество единиц в каждой группе.
Общая дисперсия () показывает вариацию во всей совокупности без учета выделения групп по факторному признаку
.
Между общей дисперсией (), средней из групповых (
) и межгрупповой дисперсией (), существует взаимосвязь, называемая «правило сложения дисперсий»
,
.
С использованием указанных дисперсий можно определить влияние факторного (группировочного) признака на вариацию результативного.
Оценка влияния основывается на расчете коэффициента детерминации или эмпирического корреляционного отношения (η)
.
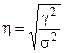Если η>0,5 это свидетельствует о влиянии факторного признака на вариацию результативного признака.
Статистические таблицы и графики
Статистическая таблица – таблица, содержащая сводную характеристику исследуемой совокупности по одному или нескольким существенным признакам, взаимосвязанным логикой статистического анализа.
Макет таблицы – заполненный заголовками скелет таблицы. Схема макета таблицы представлена на рис. 1.6.
Название таблицы (общий заголовок)
| Содержание строк | Наименование граф (верхние заголовки) | |||
| А | 3 и т.д. | |||
| Наименование строк (боковые заголовки) | Клетка таблицы | |||
| Итоговая строка | Итоговая графа |
Рис. 1.6. Схема макета статистической таблицы
Подлежащим таблицы называется объект, характеристика которого представлена в таблице. Обычно, подлежащее таблицы дается в левой части, в наименовании строк.
Сказуемое таблицы – система показателей, которыми характеризуется объект изучения, т.е. подлежащее таблицы, сказуемое, в большинстве случаев, формирует верхние заголовки и составляет содержание граф.
Шапка таблицы – совокупность подлежащего и сказуемого таблицы.
В зависимости от структуры подлежащего таблицы могут быть простые и сложные. Сложные таблицы, в свою очередь, подразделяются на групповые и комбинационные.
Простой называется таблица, в подлежащем которой дается перечень каких-либо объектов или территориальных единиц.
В групповых таблицах подлежащее содержит группировку единиц совокупности по одному количественному или атрибутивному признаку.
Комбинационная таблица позволяет охарактеризовать типические группы, выделенные по нескольким признакам и связь между ними.
По структурному строению сказуемого различают таблицы с простой и сложной его разбивкой.
При простой разработке сказуемого показатель, определяющий его, не подразделяется на подгруппы и итоговые значения получаются путем простого суммирования значений по каждому признаку отдельно, независимо друг от друга.
Сложная разработка сказуемого предполагает деление признака, формирующего его на подгруппы. При этом получается более полная и подробная характеристика объекта.
Правила построения таблиц включают в себя:
1. Таблица должна быть компактной и содержать только те данные, которые непосредственно отражают исследуемое явление в статике или динамике и необходимы для познания его сущности.
2. Заголовки таблицы должны быть четкими, краткими, лаконичными; представлять собой законченное целое, органично вписывающееся в содержание текста.
3. Графики и строки следует нумеровать. Графы, заполненные наименованием строк, принято обозначать буквами алфавита, а все последующие графы – цифрами в порядке возрастания.
4. При изложении цифрового материала должна соблюдаться одинаковая степень точности для всех чисел (одинаковое округление).
5. При заполнении таблиц используются следующие условные обозначения: при отсутствии явления «-», если нет информации о явлении «…» или «нет сведений», если изучаемое значение признака не имеет осмысленного содержания «х».
При наличии информации по изучаемому явлению, числовое значение которого составляет величину меньше принятой в таблице точности, принято записывать «0,00».