Регрессионный анализ

Статистический анализ взаимосвязей явлений

Лекция № 17

Любое явление находится в связи с другими явлениями. Исследование таких взаимосвязей – важнейшая задача статистики.

Различают два вида связей, существующих между явлениями,

Функциональной называется зависимость, при которой одному значению факторного признака строго соответствует единственное значение результативного признака.

Стохастическая зависимость характеризуется тем, что результативный признак неполностью определяется факторным признаком, его влияние проявляется в среднем при достаточно большом числе наблюдений.

Наиболее часто для исследования стохастических зависимостей используют метод корреляции.

Термин корреляция происходит от английского слова correlation – соотношение, соответствие.

К изучению связи методом корреляции обращаются в том случае, когда нельзя изолировать влияние посторонних факторов. При этом число наблюдений должно быть достаточно велико, так как малое число наблюдений не позволяет обнаружить закономерность связи.

Первая задача корреляции заключается в математическом выражении изменения результативного признака в связи с изменением одного или несколько факторных признаков. Данная задача решается определением уравнения регрессии и носит название регрессионного анализа. Вторая задача состоит в определении степени влияния искажающих факторов –различных показателей тесноты связи и называется корреляционным анализом.

Регрессионный анализ включает в себя этапы:

1. Логический анализ – разделение коррелирующих признаков на факторные и результативный.

2. Определение типа зависимости. Корреляционная зависимость называется парной, если она имеет место между двумя признаками (факторным и результативным), и множественной (многофакторной) – между тремя и более связанными между собой признаками.

Парная зависимость называется прямолинейной, если может быть описана уравнением прямой линии и криволинейной, описываемой уравнением:

гиперболы ,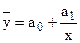

параболы и т.д.

Определить тип уравнения зависимости можно, исследуя зависимость графически, построением корреляционного поля или эмпирической линии регрессии.

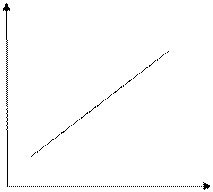
При построении корреляционного поля в системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат – результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой, как это показано на рис. 1.4.

y

 

 

x

Рис. 1.4. График корреляционного поля

 

При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем теснее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связей.

Эмпирическая линия регрессии строится в системе координат, где на оси абсцисс откладывается значение факторного признака, а на оси ординат рассчитанное среднее для данного факторного признака значение результативного.

3. Определение параметров уравнения регрессии.

Оценка параметров уравнения регрессии (а₀, а₁, а₂ и т.д.) осуществляется методом наименьших квадратов на основе системы нормальных уравнений.

Для нахождения параметров линейной парной регрессии () система нормальных уравнений имеет вид:

.

Для гиперболы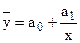

.

 

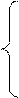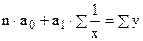
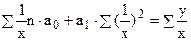Для параболы второго порядка

.

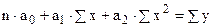
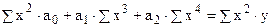Для многофакторной зависимости:

.

 

……………………………………………………………………

.

 

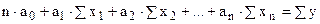
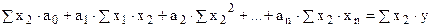
В уравнениях регрессии параметр а₀ показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков, а коэффициенты регрессии а₁, а₂, …, а_n показывают, на сколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу собственного измерения.