Изучение взаимосвязи экономических явлений.

Тема 9

В экономике многие процессы взаимосвязаны. Важно не только установить факт взаимосвязи, но и в целях прогнозирования и эффективного управления необходимо выявленным связям придавать математическую количественную определенность. Это и есть основная задача статистики в области изучения взаимосвязи. При этом одни показатели выступают как факторы (причины), то есть они обуславливают изменения других показателей, которые называются результативными. Разделение показателей на факторные и результативные условно и зависит от цели статистического изучения взаимосвязи. Взаимосвязи разделяются по характеру, зависимости, по методу изучения связи.

Одной из важных задач статистики является исследование существующих связей между явлениями. Связи могут быть:

– функциональными – когда определенному значению факторного признака соответствует одно значение результативного признака, то есть это жесткая связь, определяемая какими-то соотношениями, зависимостями или формулами, однозначная связь;

– стохастическими – причинная зависимость проявляется не в каждом отдельном случае, а, в общем, при большом числе наблюдений.

Стохастическая связь может быть:

- регрессионной, то есть связь, в которой изменение одной величины обусловлено влиянием одного или нескольких независимых факторов, а прочие факторы принимаются за постоянные или средние значения;

- корреляционной, то есть когда одной и той же величине факторного признака соответствуют несколько различных значений результативного признака или наоборот. Она проявляется не в каждом отдельном случае, а в массе случаев в средних величинах в форме тенденции. Например: связь между издержками обращения и выручкой магазина, зависимость между производительностью труда и уровнем квалификации персонала, между урожайностью зерновых и количеством выпавших осадков и т.п.

Виды связей можно разделить на три группы:

1. По направлению действия:

– прямые (с увеличением или уменьшением факторного признака соответственно увеличивается или уменьшается результативный показатель);

– обратные (с увеличением или уменьшением факторного признака соответственно уменьшается или увеличивается результативный показатель).

2. По аналитическому выражению:

– прямолинейные (связь может быть приближенно выражена уравнением прямой);

– криволинейные (связь может быть приближенно выражена уравнением кривой).

3. По количеству факторов:

– однофакторные (парные);

– многофакторные (множественные).

Таким образом, оценка степени взаимосвязей между экономическими явлениями или процессами одна из важнейших задач экономико-статистического метода. Виды связи: функциональная и стохастическая (регрессионная и корреляционная), прямые и обратные, прямолинейные и криволинейные, однофакторные и многофакторные.

1.Дисперсионный анализ.

Дисперсионный анализ является одним из методов изучения влияния одного или нескольких факторных признаков на результативный признак. В зависимости от количества факторов дисперсионный анализ подразделяется на однофакторный и многофакторный. Ниже рассмотрено применение дисперсионного анализа для случая однофакторного комплекса.

В основе дисперсионного анализа лежит расчленение общей вариации изучаемого признака по источникам ее происхождения на два вида вариации:

- систематическую вариацию, обусловленную изменением признака-фактора;

- остаточную (случайную) вариацию, обусловленную действием прочих, случайных, не связанных с данным фактором обстоятельств.

Для разграничения этих вариаций всю совокупность наблюдавшихся единиц разбивают на группы (классы) по факторному признаку и исчисляют средние результативного признака по группам.

Групповые средние: , общая средняя: .

где 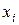– индивидуальные значения признака в группе;

– число единиц, входящих в группу;

– общее число наблюдений.

Если сравнение групповых средних показывает определенное различие в их уровне, то необходимо установить, является ли это различие существенным и вызвано ли оно влиянием признака-фактора.

Для ответа на поставленный вопрос определяют два показателя дисперсии:

1) показатель , характеризующий колеблемость групповых средних вокруг общей средней (межгрупповая дисперсия);

2) показатель , отражающий остаточную, внутригрупповую дисперсию.

Внутригрупповая - измеряет вариацию признака внутри группы

,

где - групповая средняя.

Она измеряет вариацию, обусловленную признаком, положенным в основу группировки.

Полученные показатели межгрупповой и внутригрупповой дисперсии сравнивают, получая фактическое дисперсионное отношение:

,

При дисперсионном анализе межгрупповую и внутригрупповую дисперсии определяют путем деления суммы квадратов отклонений на соответствующее число степеней свободы.

Число степеней свободы – это число внутренних и внешних факторов, которые можно изменять без изменения элементов системы.

Для межгрупповой дисперсии число степеней свободы равно числу групповых средних минус единица.

Для внутригрупповой дисперсии число степеней свободы – это разность общего числа наблюдений и числа групповых средних.

По таблице F-распределения Фишерапри определенном уровне значимости (или доверительной вероятности) и числе степеней свободы (и ) определяется табличное дисперсионное отношение ().

Если , то следует считать, что гипотеза о влиянии признака-фактора не опровергается.

Дисперсионный анализ позволяет оценить влияние одного или нескольких факторов на результативный признак. Если сравнение групповых средних в течение длительного времени показывает значительное и существенное различие в их уровне, то оно вызвано влиянием постоянного неучтенного фактора или факторов (это системная вариация). В противном случае это случайная вариация. Если при учете этого фактора сравнение групповых средних в течение продолжительного времени показывает не значительное различие в их уровне, то можно считать подтвержденным, что выявленная величина влияния фактора на результативный признак принадлежит именно ему.

2.Сущность корреляционно-регрессионной модели, условия и этапы ее составления

Корреляционно-регрессионный анализ предполагает измерение тесноты, направления связи и установление аналитического выражения (формы) связи.

Теоретическая обоснованность моделей взаимосвязи, построенных на основе корреляционно-регрессионного анализа, обеспечивается соблюдением следующих основных условий:

1. Все признаки и их совместные распределения должны подчиняться нормальному закону распределения.

2. Дисперсия моделируемого признака должна все время оставаться постоянной при изменении величины и значений факторных признаков.

3. Отдельные наблюдения должны быть независимыми, т.е. результаты, полученные в i-м наблюдении, не должны быть связаны с предыдущими и содержать информацию о последующих наблюдениях, а также влиять на них.

Этапы составления корреляционно-регрессионной модели:

1. Проводится логический анализ сущности изучаемого явления и причинно-следственных связей в результате которого устанавливается результативный показатель и факторы, влияющие на его изменение.

Число факторных признаков должно быть оптимальным. При исключении несущественных факторов модель упрощается, а ее качество не ухудшается. Но построение модели малой размерности приводит к построению модели недостаточно описывающей изучаемое явление. При построении модели число факторных признаков должно быть в 5-6 раз меньше объема изучаемой совокупности.

Парная регрессия характеризует связь между двумя признаками. Аналитическая связь между ними может быть описана в виде моделей, представленных в таблице 23

Таблица 23

Виды моделей парной регрессии

№ п/п	Наименование функции	Вид функции	Система нормальных уравнений для нахождения параметров уравнения
	Линейная
	Парабола второго порядка

 

 

Продолжение таблицы 23

	Парабола третьего порядка
	Показательная
	Гиперболическая

 

Изучение связи между тремя и более признаками называют множественной регрессией. Уравнение линейной множественной регрессии имеет вид:

.

Для нахождения параметров данного уравнения составляют систему:

 

 

2. Сбор первичной информации и проверка ее на однородность и нормальность распределения.

Однородная совокупность – совокупность, у которой коэффициент вариации не превышает 33 %.

Проверка нормальности распределения проводится с помощью правила «трех сигм» (табл. 24).

Таблица 24

Правило «трех сигм»

Интервалы значений признака-фактора	Число единиц в интервале	Удельный вес, входящих в интервал единиц в общем их числе, %	Удельный вес, входящих в интервал единиц при нормальном распределении, %
–			68,3
–			95,4
–			99,7

Сопоставление последних двух колонок позволяет судить о нормальности распределения. Но, даже не смотря на отклонения в этих столбцах, не следует отказываться от применения корреляционного анализа.

3. Исключение из массива первичной информации всех резко выделяющихся (аномальных) единиц по уровню признаков-факторов. На этом шаге исключаются единицы у которых уровень признака-фактора не попадает в интервал .

4. Установление факта наличия корреляционной зависимости между результативным и факторным признаками и определяется ее характер и направление. Для установления наличия корреляционной связи существуют специальные методы, такие как:

– анализ параллельных рядов – сопоставляют две или несколько статистические величины.

– аналитические группировки – все единицы совокупности разбиваются на группы по величине факторного признака и для каждой группы определяется средняя величина результативного показателя, затем строится график эмпирической линии регрессии, по которой можно судить о наличии связи и ее форме;

– графический метод – на графике изображается поле корреляции. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.