Группа подобий евклидова пространства
Ordm;.
Определитель Грама. Объем в евклидовом пространстве
Определение 1: пусть 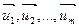 - произвольная система векторов
- произвольная система векторов 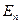 . Определителем Грама этой системы векторов называется определитель m-го порядка вида:
. Определителем Грама этой системы векторов называется определитель m-го порядка вида:
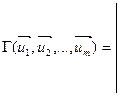
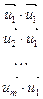
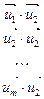

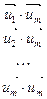
 (1)
(1)
Грам Йёрген (1850-1916) - датский математик. Определитель Грама обладает свойствами (доказаны в алгебре):
1) он всегда неотрицателен;
2) система векторов  ,
, 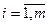 , линейно независима тогда и только тогда, когда её определитель Грама положителен.
, линейно независима тогда и только тогда, когда её определитель Грама положителен.
Замечание 1: из аналитической геометрии известно, что объем параллелепипеда, построенного на трёх неколлинеарных векторах  равен произведению площади параллелограмма, построенного на векторах
равен произведению площади параллелограмма, построенного на векторах 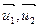 , и длины перпендикуляра, опущенного из конца вектора
, и длины перпендикуляра, опущенного из конца вектора  на плоскость векторов
на плоскость векторов 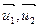 .
.
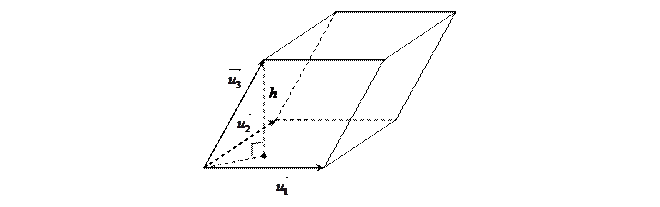

Обобщим понятие объёма трехмерного параллелепипеда на случаи больших размерностей.
Как известно, в пространстве 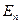 , параллелепипедом, построенным на m - линейно независимых векторах
, параллелепипедом, построенным на m - линейно независимых векторах 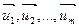 , называется множество векторов вида
, называется множество векторов вида 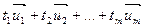 , где параметры
, где параметры  ,
, 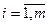 , независимо друг от друга изменяются на отрезке
, независимо друг от друга изменяются на отрезке 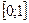 . Назовём основанием этого параллелепипеда (m-1) - мерный параллелепипед натянутый на векторы
. Назовём основанием этого параллелепипеда (m-1) - мерный параллелепипед натянутый на векторы 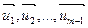 , а расстояние от конца вектора
, а расстояние от конца вектора  до плоскости
до плоскости  , натянутой на векторы
, натянутой на векторы 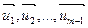 , назовём высотой исходного параллелепипеда. «Объёмом» одномерного параллелепипеда
, назовём высотой исходного параллелепипеда. «Объёмом» одномерного параллелепипеда  назовем длину вектора
назовем длину вектора  . Для больших размерностей объём определим индуктивно, как объём основания, умноженной на высоту.
. Для больших размерностей объём определим индуктивно, как объём основания, умноженной на высоту.
Теорема 1: квадрат объёма m-мерного параллелепипеда равен определителю Грама совокупности векторов 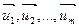 :
:
 (2)
(2)
□ Применим метод математической индукции по числу m векторов.
1) Для m=1 имеем:  - утверждение теоремы справедливо.
- утверждение теоремы справедливо.
2) Докажем что теорема имеет место для (m-1) векторов и докажем ёё справедливость для m векторов. Обозначим через  ортогональную проекцию вектора
ортогональную проекцию вектора  на ортогональное дополнение
на ортогональное дополнение 
 к подпространству
к подпространству  , натянутому на векторы
, натянутому на векторы 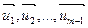 . Эта проекция осуществляется параллельно подпространству
. Эта проекция осуществляется параллельно подпространству  , поэтому
, поэтому
 ,
,  ,
,
причём  (3)
(3)
Прибавим к последнему столбцу определителя Грама (1) предшествующие столбцы, соответственно умноженные на коэффициенты  . Так как скалярное произведение линейно по второму аргументу, то получим в последнем столбце числа
. Так как скалярное произведение линейно по второму аргументу, то получим в последнем столбце числа  , причём первые (m-1) из них равны нулю (
, причём первые (m-1) из них равны нулю ( - ортогональная проекция на
- ортогональная проекция на  ). Последний элемент последнего столбца равен
). Последний элемент последнего столбца равен
 .
.
Длина вектора  равна высоте параллелепипеда, поэтому
равна высоте параллелепипеда, поэтому
 (4)
(4)
Согласно индуктивному предположению определитель Грама из правой части равенства (4) есть квадрат объёма основания. Следовательно:

и теорема доказана. ■
2º.Объём n-мерного параллелепипеда в n-мерном евклидовом пространстве
Пусть в пространстве 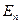 задана линейно независимая система из n-векторов
задана линейно независимая система из n-векторов  , а матрица А=(
, а матрица А=(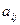 ),
),  , имеет своими столбцами координаты этих векторов
, имеет своими столбцами координаты этих векторов  в некотором ортонормированном базисе
в некотором ортонормированном базисе  . Тогда для матрицы
. Тогда для матрицы  рассмотрим элемент
рассмотрим элемент  .
.  . То есть матрица
. То есть матрица 
 является матрицей Грама системы векторов
является матрицей Грама системы векторов  .
.
Так как 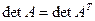 , то
, то  (5)
(5)
Из равенства (2) следует что  .
.
Теорема 2: квадрат объёма n-мерного параллелепипеда равен квадрату определителя матрицы  или
или  . (6)
. (6)
§14. Группа движений евклидова пространства
Определение 1: движением пространства 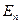 называется его аффинное преобразование, не меняющее расстояние между точками.
называется его аффинное преобразование, не меняющее расстояние между точками.
Замечание 1: из определения расстояния между точками (§11) следует, что ассоциированное с движением векторное преобразование сохраняет длины векторов, значит, является ортогональным преобразованием, кроме того при этом преобразовании не меняются скалярное произведение и углы между векторами.
Определение 2: система координат  называется прямоугольной декартовой или ортонормированной, если векторы
называется прямоугольной декартовой или ортонормированной, если векторы 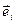 образуют ортонормированный базис векторного евклидова пространства
образуют ортонормированный базис векторного евклидова пространства  , связанной с
, связанной с 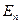 .
.
Замечание 2: при движении ортонормированная система координат отображается также на ортонормированную систему координат.
Следующие теоремы являются непосредственными следствиями аналогичных теорем из §8 и теоремы (3) из §10.
Теорема 1: при движении пространства 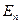 координаты
координаты  произвольной точки М и координаты
произвольной точки М и координаты  её образа М
её образа М в одной и той же ПДСК связаны формулами вида:
в одной и той же ПДСК связаны формулами вида:
 (1)
(1) 
где матрица ( ) ортогональна.
) ортогональна.
Если  , то движение (1) I рода, если же
, то движение (1) I рода, если же  , то это движение II рода.
, то это движение II рода.
Теорема 2: всякое преобразование пространства  вида (1) с ортогональной матрицей (
вида (1) с ортогональной матрицей ( ), является движением.
), является движением.
Теорема 3: движение пространства  вполне определяется заданием двух соответствующих ортонормированных систем координат (реперов).
вполне определяется заданием двух соответствующих ортонормированных систем координат (реперов).
Теорема 4: множество движений пространства Еn является группой.
□ 1) Так как движения  и
и  - аффинные преобразования, то и их композиция
- аффинные преобразования, то и их композиция  - аффинное преобразование согласно теореме (1) из §9. Так как
- аффинное преобразование согласно теореме (1) из §9. Так как  и
и  не меняют расстояний между точками, то
не меняют расстояний между точками, то  также не меняют расстояний между точками, а значит, является движением.
также не меняют расстояний между точками, а значит, является движением.
2) Так как движение  - аффинное преобразование, то
- аффинное преобразование, то  - также аффинное преобразование. Так как
- также аффинное преобразование. Так как  сохраняет расстояние между точками, то
сохраняет расстояние между точками, то  также сохраняет расстояние между точками, а значит, является движением. ■
также сохраняет расстояние между точками, а значит, является движением. ■
Рассмотрим подгруппы группы движений.
1º. Параллельный перенос задается формулами вида:
 где
где 
то есть формулами  .
.
Следовательно, матрица ( ) является единичной. Но единичная матрица ортогональна и по теореме (2) параллельный перенос является движением. Группа параллельных переносов является подгруппой группы движений пространства Еn.
) является единичной. Но единичная матрица ортогональна и по теореме (2) параллельный перенос является движением. Группа параллельных переносов является подгруппой группы движений пространства Еn.
2º. Движение, оставляющее неподвижной некоторую точку S, называется вращением вокруг центра S. Вращение является частным случаем центроаффинного преобразования (§9). Его формулы имеют такой же вид, что и формулы центроаффинного преобразования, но матрица ( ) ортогональна. Очевидно, вращение с данным центром S образуют подгруппу группы всех движений пространства Еn.
) ортогональна. Очевидно, вращение с данным центром S образуют подгруппу группы всех движений пространства Еn.
Как и в §9 указывается, что любое движение может быть представлено в виде композиции вращения и параллельного переноса.
Определение 3: Евклидовой геометрией называется наука, изучающая те свойства пространства Еn, которые не изменяются при любых движениях этого пространства.
Замечание 3: элементарная геометрия – это евклидова геометрия пространств Е2 и Е3. Так как движение является частным случаем аффинного преобразования, то любое свойство фигуры, сохраняющееся при любом аффинном преобразовании, будет сохраняться и при движении. Поэтому все свойства фигур, изучаемые в аффинной геометрии, изучаются также и в евклидовой геометрии. Однако евклидова геометрия значительно богаче по содержанию, чем аффинная геометрия, так как в ней рассматриваются метрические понятия, отсутствующие в аффинной геометрии.
Определение 1: подобием пространства Еп называется его аффинное преобразование, при котором все расстояния между точками умножаются на одно и то же положительное число k, называемое коэффициентом подобия.
Определение 2: фигура F1 называется подобной фигуре F2, если существует подобие, отображающее F1 на F2.
Пример: любое движение является подобием с коэффициентом k=1.
Теорема 1: гомотетия с коэффициентом k ≠ 0 является подобием с коэффициентом |k|.
□ Гомотетия с центром S(Si) и коэффициентом k задается в аффинной, в частности, прямоугольной декартовой системе координат формулами вида:
(1)  (см. §9)
(см. §9)
Пусть точки M(xi) и N(yi) отображаются при гомотетии соответственно на точки M'(xi) и N'(yi). Так как  , то по формуле расстояния между точками получаем:
, то по формуле расстояния между точками получаем:  ■
■
Теорема 2: множество подобий пространства Еп является группой.
□ 1) Пусть  и
и  - подобия с коэффициентами k1 и k2. Так как это аффинное преобразование, то и их композиция
- подобия с коэффициентами k1 и k2. Так как это аффинное преобразование, то и их композиция  - аффинное преобразование. При подобии
- аффинное преобразование. При подобии  все расстояния умножаются на коэффициент k1, а при подобии
все расстояния умножаются на коэффициент k1, а при подобии  все расстояния умножаются на k2, тогда при
все расстояния умножаются на k2, тогда при  все расстояния умножаются на
все расстояния умножаются на  .
.
Значит,  - подобие с коэффициентом k1∙k2.
- подобие с коэффициентом k1∙k2.
2) Пусть  - подобие с коэффициентом k. Так как это аффинное преобразование, то и
- подобие с коэффициентом k. Так как это аффинное преобразование, то и  - аффинное преобразование. При
- аффинное преобразование. При  все расстояния умножаются на число k, при
все расстояния умножаются на число k, при  они умножаются на число
они умножаются на число  , поэтому
, поэтому  является подобием. ■
является подобием. ■
Теорема 3: всякое подобие с коэффициентом k можно представить в виде композиции гомотетии (с тем же коэффициентом и любым центром) и некоторого движения.
□ Пусть  - подобие с коэффициентом k, а g – гомотетия с этим же коэффициентом. Тогда
- подобие с коэффициентом k, а g – гомотетия с этим же коэффициентом. Тогда  - гомотетия с коэффициентом
- гомотетия с коэффициентом  . Преобразование
. Преобразование  (2), является композицией подобия с коэффициентами k и
(2), является композицией подобия с коэффициентами k и  , есть подобие с коэффициентом k∙
, есть подобие с коэффициентом k∙ =1, то есть движение. Но тогда получаем из формулы (2):
=1, то есть движение. Но тогда получаем из формулы (2):  и требуемое доказано. ■
и требуемое доказано. ■
Следующие три теоремы выражают свойства подобий.
Теорема 4: при подобии с коэффициентом k длины всех векторов умножаются на число k, а все скалярные произведения векторов на k2.
□ Воспользуемся теоремой (3):  . Так как векторное преобразование, ассоциирование с движением t, является ортогональным, то оно не меняет длин и скалярных произведений векторов (см. §10).
. Так как векторное преобразование, ассоциирование с движением t, является ортогональным, то оно не меняет длин и скалярных произведений векторов (см. §10).
Векторное произведение, ассоциированное с гомотетией g, имеет вид:  , тогда при нем все длины векторов умножаются на k, а все скалярные произведения на k2.
, тогда при нем все длины векторов умножаются на k, а все скалярные произведения на k2.
 ,
,  . ■
. ■
Теорема 5: подобие не изменяет углы между векторами.
□ Пусть  , тогда
, тогда 
Так как по определению угла между векторами  и
и  , то
, то  . ■
. ■
Теорема 6: подобие с коэффициентом k задается в прямоугольной декартовой системе координат формулами вида:  , (3) где
, (3) где  , а матрица (
, а матрица ( ) ортогональна.
) ортогональна.
□ Согласно теореме (3) данное подобие представимо в виде композиции гомотетии центром в начале координат и коэффициентом k:
 (4)
(4)
и некоторого движения:  (5)
(5)
Подставляя значения (4) в (5), получаем (3). ■