Плоскости в евклидовом пространстве
Определение r-мерной плоскости и её аффинные свойства, рассмотренные ранее, сохраняются и в пространстве Е . (однако, в E
. (однако, в E имеются ряд задач специфического, метрического содержания. Обобщим некоторые метрические понятия трехмерного пространства на евклидово пространство
имеются ряд задач специфического, метрического содержания. Обобщим некоторые метрические понятия трехмерного пространства на евклидово пространство  измерений.
измерений.
Определение 1:пусть V - векторное евклидово пространство, связанное с пространством E
- векторное евклидово пространство, связанное с пространством E и W
и W - его подпространство. Множество W
- его подпространство. Множество W всех векторов из V
всех векторов из V , ортогональных любому вектору
, ортогональных любому вектору 
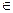 W
W , называется ортогональным дополнением пространства W
, называется ортогональным дополнением пространства W .
.
Пример:если V = {
= { },то {
},то { }
} = V
= V .
.
Определение 2:пусть V и V
и V - подпространства векторного пространства V
- подпространства векторного пространства V , где 0
, где 0  r
r  n и 0
n и 0  s
s  n. Их объединение V
n. Их объединение V , состоящее из векторов вида
, состоящее из векторов вида  +
+ , где
, где 
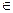 V
V , а
, а 
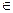 V
V , является векторным пространством и называется алгебраической суммой пространств V
, является векторным пространством и называется алгебраической суммой пространств V и V
и V и обозначается V
и обозначается V = V
= V + V
+ V .
.
Определение 3: если V
 V
V ={
={ },то алгебраическая сумма называется прямой суммой и обозначается V
},то алгебраическая сумма называется прямой суммой и обозначается V
 V
V .
.
В курсе линейной алгебры доказано следующее:
Теорема 1:для любого подпространства V
 V
V его ортогональное дополнение
его ортогональное дополнение  также является подпространством пространства V
также является подпространством пространства V , причем, если V
, причем, если V
 V
V и V
и V
 {
{ }, то V
}, то V = V
= V

 и
и  .
.
Определение 4: пусть P - многомерная плоскость пространства E
- многомерная плоскость пространства E , натянутая на точку М и векторное евклидово подпространство V
, натянутая на точку М и векторное евклидово подпространство V . Плоскость, направляющим подпространством которой служит V
. Плоскость, направляющим подпространством которой служит V , называется ортогональным дополнением к плоскости P
, называется ортогональным дополнением к плоскости P и обозначается P
и обозначается P .
.
Теорема 2: плоскости P и P
и P пространства E
пространства E пересекаются в единственной точке.
пересекаются в единственной точке.
□ Пусть P натянута на точку М и векторное евклидово подпространство V
натянута на точку М и векторное евклидово подпространство V , а плоскость P
, а плоскость P - на точку N и V
- на точку N и V . Тогда
. Тогда 
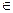 V
V
 V
V = V
= V .Значит, выполнено необходимое и достаточное условие пересечения плоскостей: для объединенной системы линейных уравнений, задающих эти плоскости, равны ранги основной и расширенной матрицы. Так как размерность их пересечения t = m + (n – m) =n, то V
.Значит, выполнено необходимое и достаточное условие пересечения плоскостей: для объединенной системы линейных уравнений, задающих эти плоскости, равны ранги основной и расширенной матрицы. Так как размерность их пересечения t = m + (n – m) =n, то V
 V
V = {
= { }, значит, P
}, значит, P и P
и P пересекаются, причем в единственной точке. ■
пересекаются, причем в единственной точке. ■
Теорема 3: через любую точку N пространства E проходит единственное ортогональное дополнение P
проходит единственное ортогональное дополнение P к плоскости P
к плоскости P , натянутой на точку M и подпространство V
, натянутой на точку M и подпространство V .
.
□ По условию плоскость P натянута на точку N и подпространство V
натянута на точку N и подпространство V , а так как многомерная плоскость вполне задается своей любой точкой и направляющим подпространством, то P
, а так как многомерная плоскость вполне задается своей любой точкой и направляющим подпространством, то P - единственна. ■
- единственна. ■
Теоремы 1-3 позволяют ввести понятие расстояния от точки до плоскости P
1  m
m  n-1.
n-1.
Пусть плоскость P натянута в пространстве E
натянута в пространстве E на точку М и подпространство V
на точку М и подпространство V плоскость P
плоскость P проходит через некоторую точку N, точка K = P
проходит через некоторую точку N, точка K = P
 P
P , точка B – произвольная точка плоскости P
, точка B – произвольная точка плоскости P .
.

По аксиоме треугольника имеем:  +
+ =
=  (1)
(1)
Так как по условию K, B 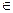 P
P , то
, то 
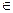 V
V ; K, N
; K, N 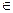 P
P , то
, то 
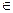 V
V , значит
, значит  и
и  =0.
=0.
Из равенства (1) по теореме Пифагора получаем:
 (2)
(2)
если B K, то
K, то  и из (2)
и из (2)  , то есть
, то есть  - длина перпендикуляра
- длина перпендикуляра  к плоскости P
к плоскости P меньше длины любой наклонной
меньше длины любой наклонной  . Поэтому расстоянием от точки N до плоскости P
. Поэтому расстоянием от точки N до плоскости P будем считать длину вектора
будем считать длину вектора  . Если же N
. Если же N 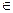 P
P , то считаем
, то считаем  . (3)
. (3)
Задача: вычислить расстояние от точки N (x
(x , x
, x ,…,x
,…,x ) до гиперплоскости P
) до гиперплоскости P c уравнением a
c уравнением a (решить на практическом занятии).
(решить на практическом занятии).
Решение: обозначим через  ортогональную проекцию точки N
ортогональную проекцию точки N на гиперплоскость P
на гиперплоскость P и выберем на ней две произвольные точки
и выберем на ней две произвольные точки  и
и  . Тогда имеем
. Тогда имеем  и
и



 , то есть
, то есть  . Значит, вектор
. Значит, вектор  ортогонален любому вектору
ортогонален любому вектору  , то есть
, то есть  и
и  . Вычислим двумя способами произведение
. Вычислим двумя способами произведение  .
.
1) =
=  , так как,
, так как,  или
или  и
и  .
.
2) =
=
 .
.
Окончательно имеем:  (4)
(4)