Аффинное преобразование в координатах
Теорема 1: при аффинном преобразовании пространства  координаты
координаты 
 произвольной точки
произвольной точки  и координаты
и координаты  ее образа
ее образа  в одной и той же аффинной системе координат связаны формулами вида
в одной и той же аффинной системе координат связаны формулами вида
 ,
,  , (1)
, (1)
то есть

при условии 
 (2)
(2)
□ Введем в пространстве  аффинную систему координат
аффинную систему координат 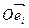 и пусть
и пусть  при аффинном преобразовании
при аффинном преобразовании  отображается на точку
отображается на точку  . Обозначим также
. Обозначим также  , где
, где  .
.


Векторное преобразование  , ассоциированное с
, ассоциированное с  , является линейным, следовательно, выражается формулами вида:
, является линейным, следовательно, выражается формулами вида:

При выполнении условия (2). По определению ассоциированного отображения, векторное отображение  отображает вектор
отображает вектор  на вектор
на вектор  . Но
. Но  ,
,  (
( ’-
’- ), тогда, подставляя координаты этих векторов вместо
), тогда, подставляя координаты этих векторов вместо  и
и  в формулы (3), получаем равенства:
в формулы (3), получаем равенства:

то есть равенство (1). ■
Замечание 1: следует отличать формулы (1) аффинного преобразования пространства  от внешне похожих на них формул преобразования координат точки (6) из теоремы (2) §2, где связаны координаты одной и той же точки в разных системах координат. Формулы же (1) связывают, вообще говоря, координаты двух различных точек (точки и её образа) в одной и той же системе координат.
от внешне похожих на них формул преобразования координат точки (6) из теоремы (2) §2, где связаны координаты одной и той же точки в разных системах координат. Формулы же (1) связывают, вообще говоря, координаты двух различных точек (точки и её образа) в одной и той же системе координат.

Теорема 2 (обратная): всякое преобразование  пространства
пространства  , выражаемое в некоторой аффинной системе координат формулами вида (1) при условии (2), является аффинным преобразование этого пространства.
, выражаемое в некоторой аффинной системе координат формулами вида (1) при условии (2), является аффинным преобразование этого пространства.
□ Пусть  - векторное пространство, связанное с данным аффинным пространством
- векторное пространство, связанное с данным аффинным пространством  . По определению аффинного преобразования достаточно показать, что для данного преобразования
. По определению аффинного преобразования достаточно показать, что для данного преобразования  существует ассоциированное с ним изоморфное преобразование
существует ассоциированное с ним изоморфное преобразование  пространства
пространства  .
.
Покажем, что таким преобразованием  является преобразовании с формулами (3).
является преобразовании с формулами (3).
Пусть при 
 и
и  отображаются соответственно на точки
отображаются соответственно на точки  и
и  , тогда имеем:
, тогда имеем:  и
и  . Но по формулам (1)
. Но по формулам (1)

Оттуда получаем:

Таким образом, координаты векторов  и
и  связаны уравнениями (3). Следовательно, преобразование
связаны уравнениями (3). Следовательно, преобразование  отображает вектор
отображает вектор  на вектор
на вектор  и поэтому ассоциировано с преобразованием
и поэтому ассоциировано с преобразованием  . Так как преобразование
. Так как преобразование  выражается формулами (3) при условии (2), то оно является изоморфным. ■
выражается формулами (3) при условии (2), то оно является изоморфным. ■
Следствие: если аффинное преобразование выражается формулами (1) при условии (2), то ассоциированное с ним векторное преобразование выражается формулами (3).
Теорема 3: для любых двух реперов  и
и  существует единственное аффинное преобразование пространства
существует единственное аффинное преобразование пространства  такое, что оно отображает точку A на точку A’,
такое, что оно отображает точку A на точку A’,  ассоциированное с ним векторное преобразование отображает базис
ассоциированное с ним векторное преобразование отображает базис  на базис
на базис  .
.
□ 1) Рассмотрим аффинную систему координат  . Из курса алгебры известно, что в векторном пространстве
. Из курса алгебры известно, что в векторном пространстве  , связанным с
, связанным с  , существует единственное преобразование
, существует единственное преобразование  , отображающее базис
, отображающее базис  на базис
на базис  . Пусть оно выражается формулами (3) при условии (2). Тогда аффинное преобразование
. Пусть оно выражается формулами (3) при условии (2). Тогда аффинное преобразование  с формулами (1), где
с формулами (1), где  , обладает всеми свойствами, перечисленными в теореме.
, обладает всеми свойствами, перечисленными в теореме.
С другой стороны, непосредственно подставляя координаты точек  в формулы (1), убеждаемся, что
в формулы (1), убеждаемся, что  .
.
2) Обратно, любое аффинное преобразование  со свойствами из формулировки теоремы совпадает с преобразованием с формулами (1). Действительно, пусть
со свойствами из формулировки теоремы совпадает с преобразованием с формулами (1). Действительно, пусть  задано формулами:
задано формулами:

Так как  , то имеем:
, то имеем:  . А так как векторное преобразование, ассоциированное с
. А так как векторное преобразование, ассоциированное с  , отображает базис
, отображает базис  на базис
на базис  , то оно совпадает с преобразованием
, то оно совпадает с преобразованием  и
и  . ■
. ■
Замечание 2: Назовем два координатных репера одноименными, если матрица перехода от одного из них к другому имеет положительныйопределитель, в противном случае (если определитель матрицы перехода отрицателен) назовём реперы разноименным. Таким образом, множество всех базисов  распадается на два непересекающихся класса. Назовем их правые и левые. При аффинном преобразовании с положительным определителем все правые системы векторов переходят в правые системы, а левые – в левые. При аффинном преобразовании с отрицательными определителем все правые системы векторов переходят в левые системы, а левые – в правые.
распадается на два непересекающихся класса. Назовем их правые и левые. При аффинном преобразовании с положительным определителем все правые системы векторов переходят в правые системы, а левые – в левые. При аффинном преобразовании с отрицательными определителем все правые системы векторов переходят в левые системы, а левые – в правые.

Определение 1: аффинное преобразование пространства  , матрица которого имеет положительный определитель, называется аффинным преобразованием I рода, а аффинное преобразование, матрица которого имеет отрицательный определитель, называется аффинным преобразованием II рода.
, матрица которого имеет положительный определитель, называется аффинным преобразованием I рода, а аффинное преобразование, матрица которого имеет отрицательный определитель, называется аффинным преобразованием II рода.