Аксиомы аффинного и n-мерного действительного пространства
I. Аффинные и евклидовы n-мерные пространства
Пусть Vn – векторное (линейное) пространство n измерений над полем действительных чисел R. Рассмотрим непустое множество E элементов произвольной природы, назовем их точками и будем обозначать заглавными буквами A,B,C … Векторы будем обозначать малыми буквами латинского алфавита со стрелкой наверху: 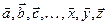 .
.
Предположим, что каждой упорядоченной паре точек A, B из E поставлен в соответствие определенный вектор  из Vn , то есть B получена при откладывании вектора
из Vn , то есть B получена при откладывании вектора  от точки A.
от точки A.
Определение 1: множество E называется аффинным n-мерным действительным пространством над векторным пространством Vn и обозначается An, если выполнены следующие аксиомы откладывания векторов:
I. Для каждой точки A из An и произвольного вектора  из Vn существует одна и только одна точка X
из Vn существует одна и только одна точка X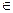 An такая, что
An такая, что  =
= .
.
II. Для любых точек A, B, C из An выполняется равенство  (аксиома треугольника).
(аксиома треугольника).
При этом пространство Vn , векторы которого сопоставляются упорядоченным парам точек из An , называется ассоциированным или связанным с пространством
An.
Замечание 1: точки пространства An и векторы пространства Vn могут иметь самую различную природу; требуется лишь, чтобы операции сложения векторов, умножения вектора на число и откладывания векторов обладали свойствами, перечисленными в сформулированных ранее аксиомах векторного пространства и аксиомам I и II аффинного пространства An.
Определение: пусть имеется непустое множество элементов, называемых векторами, в котором задана операция сложения векторов и умножения вектора на действительное число:
1)  - сумма векторов
- сумма векторов  и
и 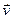
2)  и
и  - произведение вектора
- произведение вектора  на число k.
на число k.
Тогда указанное множество называется n-мерным действительным векторным пространством и обозначается Vn , если указанные две операции обладают свойствами, перечисленными в 10 аксиомах: