В ЗАМКНУТОМ ТЕОДОЛИТНОМ ХОДЕ

Цель работы: - ознакомиться со схемой обработки результатов измерений в теодолитном ходе.

Материалы, приборы и принадлежности – исходные данные, чертежные инструменты, калькулятор.

Задание:

1. Составить схему теодолитного хода.
2. Выписать исходные данные (табл. 6 и 9).
3. Обработать угловые измерения и вычислить дирекционные углы сторон.
4. Вычислить горизонтальные проложения сторон хода.
5. Вычислить приращения координат и координаты вершин хода.
6. Оценить точность сделанных вычислений.
7. Внести полученные результаты в ведомость, установленной формы (табл. 10).

Исходные данные

Для выполнения тахеометрической съемки в качестве планового обоснования был проложен замкнутый теодолитный ход (рис. 10.). Горизонтальные углы в ходе были измерены техническими теодолитами способом приемов, а длины сторон – стальными мерными лентами.

Таблица 6

№ вершины	Измеренные углы Β изм	Горизонтальные проложения, м d
	71º 35' 15"
		108,32
	51º 43' 15"
		122,91
	56º 42' 15"
		101,67

Рис.10. Схема теодолитного хода

Порядок выполнения работы

 

Камеральную обработку начинают с проверки и обработки полевых журналов. Затем составляют схему теодолитных ходов. У вершин подписывают средние значения горизонтальных углов, а возле каждой стороны – ее горизонтальную длину. На схему наносят также пункты геодезической сети, к которым осуществлялась привязка теодолитных ходов (В, 1).

Вычислительные работы по определению координат вершин теодолитного хода включают в себя:

1) Обработку угловых измерений и вычисление дирекционных углов сторон;

2) Вычисление горизонтальных проложений сторон;

3) Вычисление приращений координат и координат вершин хода.

Все вычисления ведутся в специальной ведомости. В ведомость выписывают все исходные данные и начинают обработку.

· Обработка угловых измерений и вычисление дирекционных углов сторон

1)

Вычисляют сумму измеренных углов Σ β_изм

2) Вычисляют теоретическую сумму углов Σ β_теор

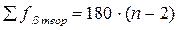где n – количество углов.

3)

Вычисляют угловую невязку f_β

4)

Полученную угловую невязку сравнивают с допустимой невязкой, т.к. величина угловой невязки характеризует точность измерения углов, она не должна быть больше предельно допустимой величины

где

Если измеренная невязка f_βизм не превышает допустимой, то вычисления продолжают. В противном случае повторяют полевые измерения.

 

5) Угловую невязку распределяют по измеренным углам поровну с обратным знаком

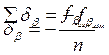При этом

(Если невязка не делится без остатка на число углов, то несколько большие поправки вводят в углы с короткими сторонами, вследствие неточности центрирования теодолита и вех).

 

6)

Вычисляют исправленные углы

Контролем правильности вычислений является равенство

 

7)

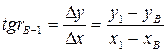Вычисляют дирекционные углы. В предложенной задачи дирекционный угол исходной стороны α_В-1 необходимо найти, решив обратную геодезическую задачу.

 

отсюда

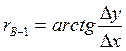Для перехода от табличного угла (r) к дирекционному (α) необходимо учесть знаки приращений координат (табл.7), определить в какой четверти лежит данное направление, учитывая знаки приращений координат. Затем, руководствуясь соотношением между табличными и дирекционным углами находят дирекционный угол направления (рис.11 и табл. 8).

Рис. 11 Связь между дирекционными углами и румбами

 

Таблица 7

Приращения координат	Дирекционный угол
0—90° (I четверть)	90—180° (II четверть)	180—270" (III четверть)	270—360° (IV четверть)
Δх	+	—	—	+
Δу	+	+	—	—

Таблица 8

Ориентирующий угол	Четверть
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (CЗ)
Румб	r1=А1	r2=180э — α	r3 = α-180°	r4 = 3603 — α
Дирекционный угол	α1= r1	α2=180э — r2	α3 = 180°+r3	α4 = 3603 — r4

 

Далее вычисляют дирекционные углы остальных сторон по формулам

α _i = α _i-1 +180˚ -β_пр (правые углы)

_, α _i = α _i-1 -180˚ + β_лев (левые углы)

где α _i-дирекционный угол определяемой стороны;

α _i-1- дирекционный угол предыдущей стороны;

β_пр - правый (левый) исправленный угол между этими сторонами.

 

Контролем правильности вычисления дирекционных углов сторон полигона является повторное получение дирекционного угла начальной стороны α_В-1.

 

· Вычисление горизонтальных проложений сторон

8) Вычисляют горизонтальные проложения сторон

d = D cos ν

и сумму горизонтальных проложений, т.е. периметр полигона Р.

 

· Вычисление приращений координат и координат вершин хода

9) Вычисляют приращения координат

Δx=d cos α

Δy=d sin α

 

10) Вычисляют суммы приращений координат ΣΔx и ΣΔy

Поскольку полигон замкнутый, то теоретическая сумма приращений координат должна быть равна нулю, т.е. Δx = 0; Δy = 0. Однако на практике вследствие погрешностей угловых и линейных измерений суммы приращений координат равны не нулю, а некоторым величинам f_x и f_y, которые называются невязками в приращениях координат f_x = ΣΔx ; f_y= ΣΔy .

В результате этих невязок полигон окажется разомкнутым на величину абсолютной линейной невязки.

Оценивают точность угловых и линейных измерений по величине относительной линейной невязки

Вычисленная относительная невязка сравнивается с допустимой

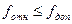(f_доп – допустимая относительная невязка устанавливается инструкциями в зависимости от масштаба съемки в пределах 1:2000 – 1:1000)

Если условие не соблюдается, то тщательно проверяют все записи и вычисления в полевых журналах и ведомостях. Если при этом ошибка не обнаружена, следует выполнить контрольные измерения длин сторон.

 

11) Выполняют уравнивание приращений координат, т.е. распределяют невязки по вычисленным приращениям координат пропорционально длинам сторон с обратным знаком. При этом поправки в приращения координат определяются по формулам:

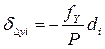
При этом Σδ_x= - f _x и Σδ_y= - f _y

12) Вычисляют исправленные приращения координат:

Δx_{i испр}= x_i+δ_∆X,

Δy_{i испр} =y_i +δ_∆У

 

13) Вычисляют суммы исправленных приращений координат, которые должны быть равны нулю:

ΣΔx_{i испр}= 0,

ΣΔy_{i испр} =0

14) По исправленным приращениям координат и координатам начальной точки последовательно вычисляют координаты вершин теодолитного хода:

Х_i+1=X_i+∆x,

У_i+1=У_i+∆y

где Х_i+1 и У_i+1 –определяемые точки;

X_i и У_i – известные координаты предыдущей точки;

∆x и ∆y – приращения координат между этими точками.

 

15) Окончательным контролем правильности вычислений координат служит получение координат начальной точки теодолитного хода.

Варианты заданий

Таблица 9