Вероятная погрешность

Частотное распределение серии измерений показывает от­клонения, т.е. погрешности, результатов измерений от среднего значения. Частотное распределение обычно отображается в ви­де, показанном на Рис. 3.3. Эта форма представления называет­ся нормальным распределением Гаусса. Такое распределение показывает, что наиболее часто встречающееся значение изме­ряемой величины, у которого нет погрешности измерения, и есть среднее значение; что малая погрешность имеет большую вероятность, чем большая; и что вероятность получить резуль­тат измерения больше среднего значения на заданную величину погрешности равна вероятности получения результата меньше среднего значения на такую же величину погрешности.

 

 

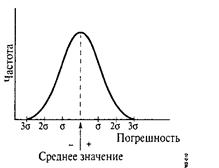
Рис. 3.3. Распределение Гаусса

 

По распределению Гаусса видно, что вероятность попадания результата измерения в интервал одного стандартного отклоне­ния от среднего значения равна 68.3%, в интервал двух стан­дартных отклонений — 95.5%, в интервал трех стандартных от­клонений — 99.7%, а четырех — 99.99%. Вероятность попада­ния результата измерения в интервал, составляющий +0.6745s от среднего значения, равна 50%. Интервал 0.6745s называется вероятной погрешностью.

Таким образом, фраза «вероятная погрешность для серии из­мерений» означает, что существует 50% вероятности того, что при произвольной выборке одного из измерений его случайное откло­нение укладывается в интервал ± 0.6745s от среднего значения.