Дивергенции
Уравнения Максвелла в дифференциальной форме
Уравнения Максвелла могут быть представлены в дифференциальной форме:
1.  ;
;
2.  ;
;
3.  ;
;
4. 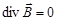 .
.
В данных уравнениях используются дифференциальные операторы:
 ,
,
и ротора
 .
.
Уравнения Максвелла в дифференциальной форме получаются из интегральных уравнений с помощью теорем Стокса и Гаусса
 ,
,
 .
.
Таким образом, уравнения Максвелла представляют собой дифференциальные уравнения в частных производных. Их значение заключается в том, что путем их решения (интегрирования) могут быть найдены сами поля  и
и  .
.
Для полного определения уравнений Максвелла в дифференциальной форме их необходимо дополнить граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Эти условия можно сформулировать в краткой форме
 ;
;  ;
;  ;
;  .
.
Фундаментальные уравнения Максвелла должны быть дополнены соотношениями, в которые входили бы величины, характеризующие индивидуальные свойства среды. Эти соотношения называются материальными уравнениями. В общем случае они могут быть крайне сложными, поэтому приведем материальные уравнения для случая изотропных сред, не содержащих сегнетоэлектриков и ферромагнетиков:
 ;
;  ;
; 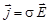 ,
,
где  – объемная плотность заряда;
– объемная плотность заряда;  – диэлектрическая проницаемость среды;
– диэлектрическая проницаемость среды;  Ф/м – электрическая постоянная,;
Ф/м – электрическая постоянная,;  – магнитная проницаемость среды;
– магнитная проницаемость среды;  Гн/м – магнитная постоянная,;
Гн/м – магнитная постоянная,; 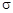 – удельная электрическая проводимость среды.
– удельная электрическая проводимость среды.