Силы Ампера и Лоренца

Закон Ампера определяет силу, действующую на проводник с током, помещенный в магнитное поле:

 

; ,

 

где – сила тока; – элемент длины провода (вектор совпадает по направлению с током ); – длина проводника. Сила Ампера перпендикулярна направлению тока и направлению вектора магнитной индукции.

Если прямолинейный проводник длиной находится в однородном поле, то модуль силы Ампера определяется выражением (рис. 3.7):

.

 

 

Рис. 3.7. Правило левой руки и правило буравчика для определения направления силы Ампера

 

Сила Лоренца (полная электромагнитная сила, действующая на заряженную частицу в электрическом и магнитном полях)

 

,

 

где 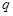– электрический заряд; – напряженность электрического поля; – скорость частицы; – индукция магнитного поля.

Только в магнитном поле на движущуюся заряженную частицу действует магнитная составляющая силы Лоренца (рис. 3.8)

 

.

 

Магнитная составляющая силы Лоренца перпендикулярна вектору скорости и вектору магнитной индукции. Она не изменяет величины скорости, а изменяет только ее направление, следовательно, работы не совершает.

Рис. 3.8. Сила Лоренца

 

Если частица влетает в магнитное поле под углом к силовым линиям , то она равномерно движется в магнитном поле по окружности радиусом и периодом обращения:

; ,

 

где – масса частицы.

Если заряженная частица влетает в однородное магнитное поле под углом , то она движется по винтовой линии (рис. 3.9).

 

 

Рис. 3.9. Движение по винтовой линии заряженной частицы в магнитном поле

 

 

Рис. 3.10. Заряженные частицы не выходят за пределы магнитной «бутылки». Поле может быть создано с помощью двух круглых витков с током

 

Отношение магнитного момента к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите,

,

 

где 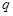‑ заряд частицы; т ‑ масса частицы.